Fläche zwischen Graph einer Funktion und x-Achse

In diesem Artikel geht es um die Berechnung der Fläche zwischen den Graph einer Funktion und der x-Achse in einem bestimmten Intervall. Dabei spielt der Begriff des 'bestimmten Integrals' eine zentrale Rolle. Wir erläutern die Flächenberechnung anhand eines Beispiels.

Es ist die reelle Funktion \(f(x)=x^2+\sin (\pi x)\) gegeben. Der Graph der Funktion ist in der nächsten Grafik eingezeichnet.

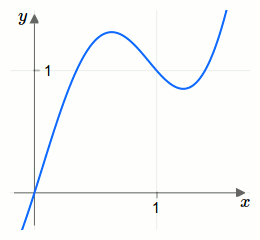
Wir bleiben beim Beispiel von vorhin. Betrachten wir weiter die Funktion von oben. Unsere Frage: Wie groß ist die Fläche zwischen der \(x\)-Achse und der Funktion im Intervall zwischen \(0{,}5\) und \(1{,}5\)?

In der nächsten Grafik zeichnen wir die Fläche ein.

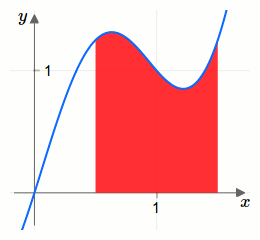
Fläche zwischen Funktion und x-Achse in einem bestimmten Intervall

Untersumme und Obersumme

Als Nächstes versuchen wir uns zu überlegen, wie man die Fläche näherungsweise berechnen kann. Dazu zeichnen wir Rechtecke ein, die von der \(x\)-Achse bis zum Funktionsgraphen reichen. Die Summe der Flächeninhalte der Rechtecke ist dann näherungsweise die Summe der roten Fläche von der vorletzten Grafik.

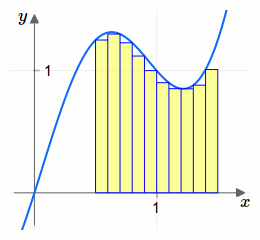
Riemann Summe - Fläche - bestimmtes Integral - Summe von Rechtecken

Die Rechtecke haben alle die gleiche Breite \(\Delta x\). Es ist \(h_1\) die Höhe des ersten Rechtecks, \(h_2\) die Höhe des zweiten Rechtecks, \(h_3\) die Höhe des dritten Rechtecks, und so weiter. Die Summe der Flächeninhalte der Rechtecke kann damit durch folgende Summe berechnet werden: \[\Delta x \cdot h_1 + \Delta x \cdot h_2 + \Delta x \cdot h_3 + ... + \Delta x \cdot h_{10}\]

Die Summe im Beispiel bezeichnet man als Summe von Produkten. Man nennt diese Summe auch Untersumme, weil die Rechtecke unterhalb des Funktionsgraphen enden. Hat man \(n\) Rechtecke gegeben so lautet die Untersumme \[U_n = \Delta x \cdot h_1 + \Delta x \cdot h_2 + \Delta x \cdot h_3 + ... + \Delta x \cdot h_n\] \[U_n = \sum _{k=1}^{n} \Delta x \cdot h_k\] Tendenziell gilt: mehr Rechtecke man einzeichnet, desto genauer wird die Summe. In der nächsten interaktiven Grafik kann man dazu die Anzahl der Rechtecke variieren.

Wir hätten die Rechtecke nun auch anders einzeichnen können. Und zwar derart, dass die Rechtecke erst oberhalb vom Funktionsgraphen enden. Genau wie vorhin ist die Summe der Flächeninhalte der Rechtecke dann näherungsweise die Summe der roten Fläche. Es ist dann \(H_1\) die Höhe des ersten Rechtecks, \(H_2\) die Höhe des zweiten Rechtecks, \(H_3\) die Höhe des dritten Rechtecks, und so weiter. Die Summe der Flächeninhalte der Rechtecke kann damit durch folgende Summe berechnet werden: \[O_n = \Delta x \cdot H_1 + \Delta x \cdot H_2 + \Delta x \cdot H_3 + ... + \Delta x \cdot H_n\] \[O_n = \sum _{k=1}^{n} \Delta x \cdot H_k\] Man nennt diese Summe Obersumme, weil die Rechtecke oberhalb der Funktion enden. In der nächsten interaktiven Grafik kann man wie zuvor die Anzahl der Rechtecke variieren.

Fläche als bestimmtes Integral

Die tatsächliche Fläche zwischen der Funktion und der \(x\)-Achse im gegebenen Intervall ist offensichtlich kleiner als die Obersumme und sie ist größer als die Untersumme. Lässt man die Anzahl der Rechtecke immer größer werden, so nähern sich die Obersumme und die Untersumme einander an. Bei unendlich vielen Rechtecken sind die Obersumme, die Untersumme und die tatsächliche Summe gleich! Hinweis: Dies gilt strenggenommen nur für Funktionen die stetig sind.

Die gesuchte Fläche \(A\) kann daher als Grenzwert der Obersumme bzw. der Untersumme aufgefasst werden. \[A=\lim _{n\rightarrow \infty} O_n\] \[A=\lim _{n\rightarrow \infty} U_n\] Man verwendet dafür ein eigenes Symbol bzw. eine eigene Schreibweise.

\[A=\int _a ^b f(x) dx\]

Das bedeutet, der Flächeninhalt \(A\) der zwischen der Funktion \(f(x)\) und der \(x\)-Achse liegt, ist durch das bestimmte Integral \(\int\) (unendliche Summe) gegeben, beginnend bei der Stelle \(a\) und endend bei der Stelle \(b\). Man nennt \(a\) und \(b\) auch Integrationsgrenzen. Das Symbol \(\int\) sieht aus wie ein großes S. S wie Summe, oder genauer unendliche Summe.

In unserem Beispiel haben wir \[A=\int _{0{,}5}^{1{,}5} (x^2+\sin (\pi x))dx\]

Überraschend ist, dass diese Fläche durch das Umkehren der Differenzierung einer Funktion ermittelt werden kann. Die Stammfunktion \(F(x)\) einer (integrierbaren) Funktion \(f(x)\) lautet nämlich \[F(x)=\int f(x) dx + c\]

\[F(x)=\frac{1}{3}x^3-\frac{1}{\pi}\cos (\pi x) + c\] Beachte, dass \(F'(x)=f(x)\). Da wir hier keine Integrationsgrenzen (\(a\) und \(b\)) haben, handelt es sich um ein unbestimmtes Integral. Damit ist das Ergebnis auch keine Fläche, sondern eine Funktion.

Möchte man eine Fläche berechnen, so kann man sich die Stammfunktion zunutze machen. Es gilt nämlich

\[A=\int _a ^b f(x) dx=F(b)-F(a)\]

Man schreibt oft \[A=\int _a ^b f(x) dx = F(x)\Big| _a ^b=F(b)-F(a)\]

Für unser Beispiel gilt daher \[A=F(b)-F(a)= \frac{1}{3}b^3-\frac{1}{\pi}\cos (\pi b) - \frac{1}{3}a^3 + \frac{1}{\pi}\cos (\pi a)\] Setzen wir \(a=0{,}5\) und \(b=1{,}5\) ein so ergibt sich \[A\approx 1{,}125 - 0{,}317 - 0{,}042 + 0{,}318\] \[A\approx 1{,}084\]

Zu den interaktiven Aufgaben → Fläche zwischen Graph einer Funktion und x-Achse - Übungsaufgaben

Weiterführende Artikel: