Winkelgeschwindigkeit

In diesem Artikel wird der Begriff 'Winkelgeschwindigkeit' eingeführt und erklärt.

Drehbewegungen kommen in der Natur und in der Technik sehr oft vor. Öfter als man vermutet. Als nächstes betrachten wir die kreisförmige Drehbewegung eines punktförmigen Objekts.

Eine grundlegende Größe bei Drehbewegungen ist die Winkelgeschwindigkeit. Sie gibt an wie schnell sich ein Objekt im Kreis dreht.

Angenommen, ein Objekt bewegt sich kreisförmig. Innerhalb eines kurzen Zeitintervalls ändert sich damit die Lage des Objekts. Der Unterschied der Positionen vor und nach dem Zeitintervall kann durch eine Winkeländerung dargestellt werden.

Die Winkelgeschwindigkeit \(\omega\) des Objekts gibt dann die Winkeländerung \(\Delta \varphi\) pro Zeitintervall \(\Delta t\) an. \[\omega=\frac{\Delta \varphi}{\Delta t}\]

In der folgenden Animation wird skizzenhaft gezeigt, wie man eine Winkelgeschwindigkeit messen kann. Man misst den Winkel (wird durch blaue Fläche dargestellt) der innerhalb einer bestimmten Zeitdauer zurückgelegt wird (eingeblendete Stoppuhr). Die Division vom Winkel durch die Zeit ergibt dann die Winkelgeschwindigkeit.

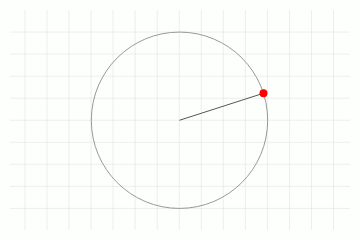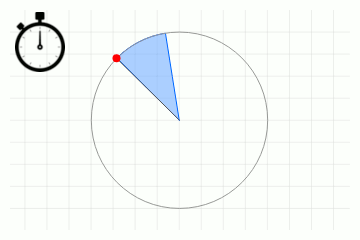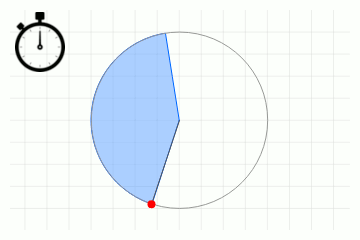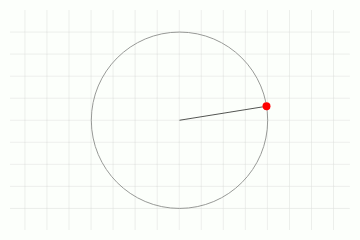
Der Sekundenzeiger einer Uhr durchläuft in 60 Sekunden eine volle Umdrehung. Damit haben wir \(\Delta t=60\) s und \(\Delta\varphi = 2\pi\) Radiant (bzw. 360 Grad). Die Winkelgeschwindigkeit lautet \[\omega=\frac{\Delta \varphi}{\Delta t}=\frac{360\text{ Grad}}{60\text{ s}}= 6\text{ Grad/s}\] Der Sekundenzeiger bewegt sich also um sechs Grad pro Sekunde im Kreis.