Lichtbrechung

In diesem Artikel wird die Lichtbrechung und das Brechungsgesetz erklärt.

Innerhalb eines homogenen Mediums breitet sich Licht geradlinig aus. Durchläuft ein Lichtstrahl jedoch verschiedene Medien (wie Glas, Wasser oder Luft), so kann es zu einer Änderung der Ausbreitungsrichtung des Lichts kommen, der sogenannten Lichtbrechung.

Licht legt immer den schnellsten Weg zwischen zwei Orten/Positionen zurück.

Da sich Licht nicht überall gleich schnell ausbreitet (beispielsweise in Glas langsamer als in Luft), und Licht immer den schnellsten Weg und nicht den kürzesten Weg zurücklegt, kommt es zur Lichtbrechung. Wenn Licht also von einem Medium in ein anderes Medium vordringt, in dem es sich mit einer anderen Geschwindigkeit ausbreitet, so wird das Licht gebrochen. Dies ergibt typischerweise einen Knick in der Ausbreitungslinie des Lichts.

Eine Lichtbrechung ist also die Änderung der Ausbreitungsrichtung von Licht aufgrund einer Änderung der Ausbreitungsgeschwindigkeit des Lichts. Die Ausbreitungsgeschwindigkeit des Lichts in einem Medium wird mit dem Brechungsindex (auch Brechzahl) des Mediums beschrieben.

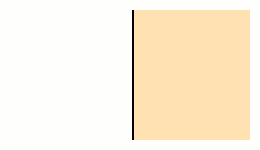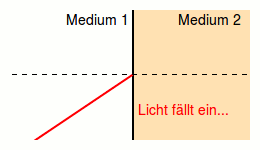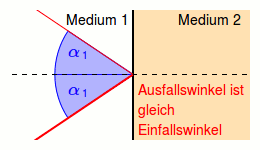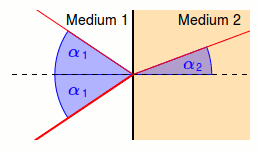
\[n=\frac{c}{c_M}\]

Dabei ist \(n\) der Brechungsindex des Mediums, \(c\) die Lichtgeschwindigkeit im Vakuum und \(c_M\) die Lichtgeschwindigkeit im Medium.

Wie lautet das Brechungsgesetz?

Zwischen unterschiedlichen Medien wie etwa Glas, Wasser oder Luft wird Licht laut dem Brechungsgesetz \[n_1\cdot \sin (\alpha_1)=n_2\cdot \sin (\alpha_2)\] gebrochen.

Dabei ist \(\alpha_1\) der Einfallswinkel und \(\alpha_2\) der Ausfallswinkel jeweils zum Lot hin gemessen (senkrecht zur Oberfläche). Weiters ist \(n_1\) der Brechungsindex des Mediums des einfallenden Strahls und \(n_2\) der Brechungsindex des Mediums des ausfallenden/gebrochenen Strahls.

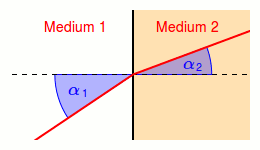
Grafik Lichtbrechung — Entlang der roten Linie fällt Licht ein. Aufgrund der unterschiedlichen Brechungsindizes der beiden Medien kommt es zur Lichtbrechung.

Warum kann es beim Übergang von Luft zu Glas zur Lichtbrechung kommen?

Da die Ausbreitungsgeschwindigkeit des Lichts im Glas geringer ist als in der Luft hat Glas einen Brechungsindex der größer ist als der Brechungsindex von Luft. Nach dem Brechungsgesetz sind dann der Einfallswinkel und der Ausfallswinkel voneinander verschieden.

Aufgaben mit Lösungen

Licht tritt mit einem Winkel von 45 Grad von Luft \(n\approx 1\) in Glas (\(n\approx 1{,}5\)) ein. Wie groß ist der Austrittswinkel?

Wir haben \(n_1=1,n_2=1{,}5,\alpha_1=45^{\circ}\). Formt man das Brechungsgesetz um und setzt diese Werte ein, so erhält man\[\sin(\alpha_2)=\frac{n_1\cdot \sin (\alpha_1)}{n_2}=0{,}33333\]Anwendung des Arcussinus ergibt\[\alpha_2=\arcsin(0{,}33333)\approx 19{,}5^{\circ}\]

Zu den interaktiven Aufgaben → Lichtbrechung - Übungsaufgaben