Parallelschaltung Widerstand
In diesem Artikel wird die 'Parallelschaltung von Widerständen' eingeführt und erklärt.
Sind mehrere elektrische Bauteile mit elektrischen Widerständen in einem Stromkreis parallel miteinander verbunden, so kann man die einzelnen Widerstände zu einem Gesamtwiderstand zusammenfassen.
Sind in einem Stromkreis zwei elektrische Widerstände, \(R_1\) und \(R_2\), parallel zueinander geschalten, so kann der elektrische Gesamtwiderstand \(R\) durch \[\frac{1}{R}=\frac{1}{R_1}+\frac{1}{R_2}\] berechnet werden.
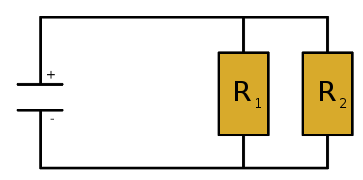
Es sind zwei Glühbirnen in einem Stromkreis parallel geschaltet. Die elektrischen Widerstände der Glühbirnen lauten \(R_1=10\Omega\) und \(R_2=15\Omega\). Wie groß ist der Gesamtwiderstand?
\[\frac{1}{R}=\frac{1}{R_1}+\frac{1}{R_2}=\frac{1}{10\Omega}+\frac{1}{15\Omega}\]
\[R=\frac{1}{\frac{1}{R_1}+\frac{1}{R_2}}=\frac{1}{\frac{1}{10\Omega}+\frac{1}{15\Omega}}=6\Omega\]
Es sind drei ohmsche Widerstände (\(R_1\), \(R_2\) und \(R_3\)) parallel geschaltet. Wie groß ist der Gesamtwiderstand?
\[\frac{1}{R}=\frac{1}{R_1}+\frac{1}{R_2}+\frac{1}{R_3}\]
\[R=\frac{1}{\frac{1}{R_1}+\frac{1}{R_2}+\frac{1}{R_3}}\]
Zu den interaktiven Aufgaben → Parallelschaltung Widerstand - Übungsaufgaben
Weiterführende Artikel:
Hat alles, was man braucht: Taschenrechner CASIO FX-991DE X *
Die mit Sternchen (*) gekennzeichneten Verweise sind sogenannte Provisions-Links. Für dich entstehen dabei keine Nachteile!