MathematikEine Asymptote einer Funktion ist eine Kurve, die sich an die Funktion annähert. Man unterscheidet zwischen
- senkrechten (vertikalen) Asymptoten
- waagrechten (horizontalen) Asymptoten
- schrägen Asymptoten
- gekrümmten Asymptoten.
Senkrechte Asymptote
Eine senkrechte Asymptote einer Funktion ist eine senkrechte Gerade mit der Eigenschaft, dass sich die Gerade und die Funktion immer weiter annähern.Die Funktion \(f(x)=\frac{1}{x}\) hat bei \(x=0\) eine senkrechte Asymptote. Der Funktionsgraph (blau) und der Graph der Asymptote (orange) sind in der folgenden Grafik dargestellt.
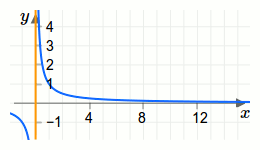
Die Logarithmusfunktion \(f(x)=\ln (x)\) hat bei \(x=0\) eine senkrechte Asymptote. Der Funktionsgraph (blau) und der Graph der Asymptote (orange) sind in der folgenden Grafik dargestellt.
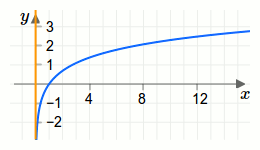
Waagrechte Asymptote
Eine waagrechte Asymptote einer Funktion ist eine waagrechte Gerade mit der Eigenschaft, dass sich die Gerade und die Funktion immer weiter annähern.Die Funktion \(f(x)=\frac{1}{x}\) hat bei \(y=0\) eine waagrechte Asymptote. Der Funktionsgraph (blau) und der Graph der Asymptote (orange) sind in der folgenden Grafik dargestellt.
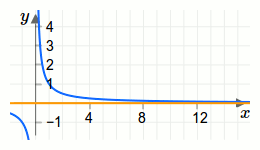
Die Exponentialfunktion \(f(x)=e^{-x}\) hat bei \(y=0\) eine waagrechte Asymptote. Der Funktionsgraph (blau) und der Graph der Asymptote (orange) sind in der folgenden Grafik dargestellt.
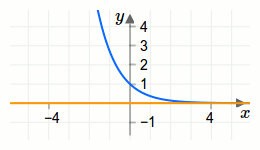
Schräge Asymptote
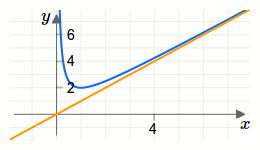
Eine schräge Asymptote einer Funktion ist eine Funktion mit der Eigenschaft, dass sich beide Funktionen immer weiter annähern.Die Funktion \(f(x)=\frac{1}{x}+x\) hat die Asymptote \(f(x)=x\). Der Funktionsgraph (blau) und der Graph der Asymptote (orange) sind in der folgenden Grafik dargestellt.
Gekrümmte Asymptote
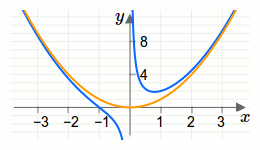
Eine Asymptote muss keine Gerade sein!Die Funktion \(f(x)=\frac{1}{x}+x^2\) hat die Asymptote \(f(x)=x^2\). Der Funktionsgraph (blau) und der Graph der Asymptote (orange) sind in der folgenden Grafik dargestellt.
Weiterführende Artikel:
Impressum
Datenschutz