---

Extremwert Definition

Ein Extremwert einer Funktion kann entweder ein Hochpunkt oder ein Tiefpunkt der Funktion sein. Zu einem Hochpunkt sagt man auch Maximum. Zu einem Tiefpunkt sagt man auch Minimum. Dabei verwendet man die unterschiedlichen Bezeichnungen globaler und lokaler Extremwert.

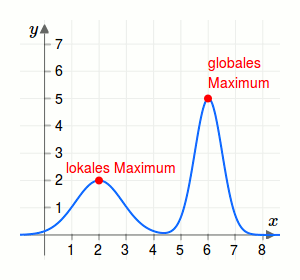
• Ist eine Funktion nirgendwo größer als an einer bestimmten Stelle, dann hat die Funktion dort einen globalen Hochpunkt.
• Ist eine Funktion nirgendwo kleiner als an einer bestimmten Stelle, dann hat die Funktion dort einen globalen Tiefpunkt.
• Eine Funktion hat an einer Stelle einen lokalen Hochpunkt, wenn in einer Umgebung um diese Stelle die Funktion nirgendwo größer ist.
• Eine Funktion hat an einer Stelle einen lokalen Tiefpunkt, wenn in einer Umgebung um diese Stelle die Funktion nirgendwo kleiner ist.

Fassen wir das Ganze in mathematischer Notation zusammen. Eine Funktion \(f: \mathbb{D}\rightarrow \mathbb{R}, x\mapsto y=f(x)\) habe an der Stelle \(x_0\) einen Extremwert.

• Ein globaler Hochpunkt \(x_0\) liegt vor, wenn für eine beliebige Zahl \(x \in \mathbb{D}\) gilt, dass \(f(x)\leq f(x_0)\).
• Ein globaler Tiefpunkt \(x_0\) liegt vor, wenn für eine beliebige Zahl \(x \in \mathbb{D}\) gilt, dass \(f(x)\geq f(x_0)\).
• Ein lokaler Hochpunkt \(x_0\) liegt vor, wenn es ein Intervall \(I\subset \mathbb{D}\) um den Hochpunkt gibt, wo für eine beliebige Zahl \(x \in I\) gilt, dass \(f(x)\leq f(x_0)\).
• Ein lokaler Tiefpunkt \(x_0\) liegt vor, wenn es ein Intervall \(I\subset \mathbb{D}\) um den Tiefpunkt gibt, wo für eine beliebige Zahl \(x \in I\) gilt, dass \(f(x)\geq f(x_0)\).

Bemerkung: An den Stellen an dem ein Monotoniewechsel gegeben ist, befindet sich auch ein lokales Maximum oder Minimum. Eventuell sind folgende Aufgaben interessant:

---

Weiterführende Artikel:

• Extrema berechnen

---