Lokale Extrema Berechnen
Lokale Extrema einer zweimal differenzierbaren Funktion können durch die erste und zweite Ableitung berechnet werden.
An einer Stelle \(x_0\) einer Funktion \(f\) befindet sich ein lokaler Hochpunkt, wenn \(f'(x_0) = 0\) und \(f''(x_0) < 0\) ist.
An einer Stelle \(x_0\) einer Funktion \(f\) befindet sich ein lokaler Tiefpunkt, wenn \(f'(x_0) = 0\) und \(f''(x_0) > 0\) ist.
Schritte zum Berechnen von lokalen Extrema:
- Berechne die Ableitungsfunktion \(f'(x)\)
- Berechne die zweite Ableitungsfunktion \(f''(x)\)
- Finde alle Nullstellen \(x_0\) der Ableitungsfunktion: Löse dazu die Gleichung \(f'(x_0)=0\)
- Untersuche Krümmung der Funktion an diesen Nullstellen:
- Ist \(f''(x_0) < 0\), dann ist bei \(x_0\) ein Hochpunkt.
- Ist \(f''(x_0) > 0\), dann ist bei \(x_0\) ein Tiefpunkt.
- Ist \(f''(x_0)=0\), dann ist bei \(x_0\) kein Extrempunkt.
Aufgaben mit Lösungen
Es ist \(f(x)=3x-x^3\) gegeben. Hat die Funktion lokale Extrema?
Die Ableitungsfunktion lautet \(f'(x)=3-3x^2\).
Die zweite Ableitungsfunktion lautet \(f''(x)=-6x\).
Wir suchen nun die Nullstellen der ersten Ableitungsfunktion. \[f'(x_0)=0\] \[3-3x_0^2=0\qquad\color{gray}{|:3}\] \[1-x_0^2=0\] Mithilfe der PQ-Formel für quadratische Gleichungen erhalten wir die beiden Lösungen \(x_0=-1\) oder \(x_0=1\). Die erste Ableitungsfunktion hat damit bei \(-1\) und \(1\) jeweils Nullstellen.
An der Stelle \(x_0=-1\) lautet die zweite Ableitung \(f''(x_0)=-6\cdot (-1)=6 > 0\).
Damit hat die Funktion dort ein Minimum.
An der Stelle \(x_0=1\) lautet die zweite Ableitung \(f''(x_0)=-6\cdot 1=-6 < 0\).
Damit hat die Funktion dort ein Maximum.
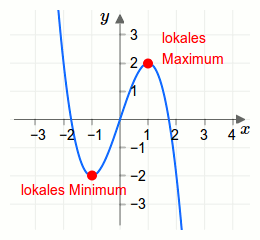
Der Funktionsgraph der Funktion \(f\) sowie das lokale Minimum und das lokale Maximum sind in der folgenden Grafik dargestellt.
Die zweite Ableitungsfunktion lautet \(f''(x)=-6x\).
Wir suchen nun die Nullstellen der ersten Ableitungsfunktion. \[f'(x_0)=0\] \[3-3x_0^2=0\qquad\color{gray}{|:3}\] \[1-x_0^2=0\] Mithilfe der PQ-Formel für quadratische Gleichungen erhalten wir die beiden Lösungen \(x_0=-1\) oder \(x_0=1\). Die erste Ableitungsfunktion hat damit bei \(-1\) und \(1\) jeweils Nullstellen.
An der Stelle \(x_0=-1\) lautet die zweite Ableitung \(f''(x_0)=-6\cdot (-1)=6 > 0\).
Damit hat die Funktion dort ein Minimum.
An der Stelle \(x_0=1\) lautet die zweite Ableitung \(f''(x_0)=-6\cdot 1=-6 < 0\).
Damit hat die Funktion dort ein Maximum.
Der Funktionsgraph der Funktion \(f\) sowie das lokale Minimum und das lokale Maximum sind in der folgenden Grafik dargestellt.
Es ist \(f(x)=x^3\) gegeben. Hat die Funktion lokale Extrema?
Die erste Ableitungsfunktion lautet \(f'(x)=3x^2\).
Die zweite Ableitungsfunktion lautet \(f''(x)=6x\).
Wir suchen nun die Nullstellen der ersten Ableitungsfunktion. \[f'(x_0)=0\] \[3x_0^2=0\qquad\color{gray}{|:3}\] \[x_0^2=0\qquad\color{gray}{|\sqrt{}}\] \[x_0=0\] Die erste Ableitungsfunktion hat bei \(x_0=0\) eine Nullstelle.
An der Stelle \(x_0=0\) lautet die zweite Ableitung \(f''(x_0)=6\cdot 0=0\).
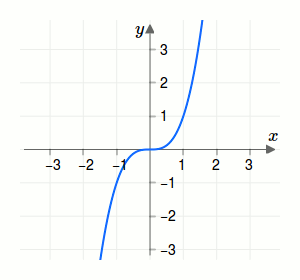
An dieser Stelle hat die Funktion weder ein Maximum noch ein Minimum, da die zweite Ableitung dort Null ist! Betrachte den entsprechenden Funktionsgraphen in der folgenden Grafik.
Die zweite Ableitungsfunktion lautet \(f''(x)=6x\).
Wir suchen nun die Nullstellen der ersten Ableitungsfunktion. \[f'(x_0)=0\] \[3x_0^2=0\qquad\color{gray}{|:3}\] \[x_0^2=0\qquad\color{gray}{|\sqrt{}}\] \[x_0=0\] Die erste Ableitungsfunktion hat bei \(x_0=0\) eine Nullstelle.
An der Stelle \(x_0=0\) lautet die zweite Ableitung \(f''(x_0)=6\cdot 0=0\).
An dieser Stelle hat die Funktion weder ein Maximum noch ein Minimum, da die zweite Ableitung dort Null ist! Betrachte den entsprechenden Funktionsgraphen in der folgenden Grafik.
Zu den interaktiven Aufgaben → Extremwert berechnen - Übungsaufgaben
Weiterführende Artikel:
Hat alles, was man braucht: Taschenrechner CASIO FX-991DE X *
Die mit Sternchen (*) gekennzeichneten Verweise sind sogenannte Provisions-Links. Für dich entstehen dabei keine Nachteile!