Monotoniewechsel einer Funktion

Ein Monotoniewechsel einer Funktion ist an einer Stelle gegeben, an der die Steigung der Funktion das Vorzeichen wechselt. Das ist genau dann der Fall, wenn die Funktion zwischen strengen Monotonien wechselt. Entweder, wenn sich die Funktion von streng monoton fallend zu streng monoton steigend ändert. Oder, wenn sich die Funktion von streng monoton steigend zu streng monoton fallend ändert. Achtung! Es muss ein Wechsel zwischen zwei strengen Monotonien sein! Der Wechsel von lediglich monoton steigend zu monoton fallend kann zwar einen Monotoniewechsel beinhalten, muss aber nicht! Denn eine konstante Funktion ist monoton steigend und monoton fallend zugleich, aber weder streng monoton steigend noch streng monoton fallend.
Betrachte dazu folgenden Funktionsgraphen der konstanten Funktion \(f(x)=4\). Er hat überall die Steigung Null und ist daher monoton steigend und monoton fallend zugleich. Er ist aber nirgendwo streng monoton fallend bzw. streng monoton steigend. Falls das nicht klar ist, sieh dir nochmals die Definition von streng monoton steigend/fallend an!

Eine konstante Funktion hat keinen Monotoniewechsel — Funktionsgraph einer konstanten Funktion.

Üblicherweise untersucht man das Monotonieverhalten einer Funktion mittels der Differentialrechnung. Dazu gehe am besten zu folgendem Artikel: Monotonie und Differentialrechnung oder betrachte das vierte Beispiel weiter unten.

Besondere Eigenschaften eines Monotoniewechsel sind:

An den Stellen wo ein Monotoniewechsel gegeben ist, befindet sich auch ein Extremwert.
An den Stellen wo sich eine Funktion von streng monoton fallend zu streng monoton steigend ändert ist ein Monotoniewechsel gegeben.
Am leichtesten kann man die Stellen mit Monotoniewechsel einer Funktion finden, wenn die Ableitungsfunktion in faktorisierter Form gegeben ist.

Aufgaben mit Lösungen

An welchen Stellen hat die Funktion \(f(x)=\frac{1}{5}\cdot (x-3)^2+2\) einen Monotoniewechsel?

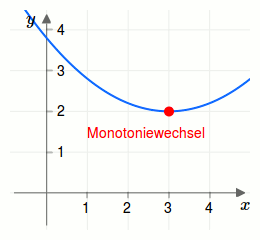
Betrachte den Funktionsgraph in der folgenden Grafik. Für alle \(x < 3\) ist die Funktion streng monoton fallend. Für alle \(x > 3\) ist die Funktion streng monoton steigend. Damit ist bei \(x=3\) ein Monotoniewechsel gegeben!

Monotoniewechsel Beispiel 1 — Figur zum ersten Beispiel.

An welchen Stellen hat die Funktion \(f(x)=\frac{1}{5}\cdot (x-4)^3-\frac{1}{2}\cdot (x-4)^2-(x-4)+5\) einen Monotoniewechsel?

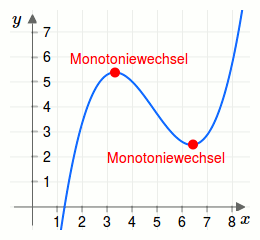
Betrachte den Funktionsgraph in der nächsten Grafik. Für alle \(x < 3{,}3\) ist die Funktion streng monoton steigend. Für alle \(3{,}3 < x < 6{,}4\) ist die Funktion streng monoton fallend. Für alle \(x > 6{,}4\) ist die Funktion streng monoton steigend. Damit sind bei \(x=3{,}3\) und bei \(x=6{,}4\) Monotoniewechsel gegeben!

Monotoniewechsel Beispiel 2 — Figur zum zweiten Beispiel.

An welchen Stellen hat die Funktion \(f(x)=\frac{1}{5}\cdot (x-2)^3+3\) einen Monotoniewechsel?

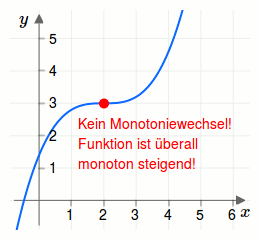
Betrachte dazu den Funktionsgraph in der nächsten Grafik. Für alle \(x < 2\) ist die Funktion streng monoton steigend. Für alle \(x > 2\) ist die Funktion streng monoton steigend. Die Steigung ist bei \(x=2\) gleich Null, also ist die Funktion überall monoton steigend. Damit hat die Funktion keinen Monotoniewechsel!

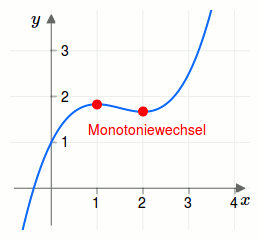
Kein Monotoniewechsel Beispiel 3 — Figur zum dritten Beispiel.

An welchen Stellen hat die reelle Funktion \(f(x)=\frac{x^3}{3}-\frac{3x^2}{2}+2x+1\) einen Monotoniewechsel?

Die Ableitungsfunktion (wie man die Ableitungsfunktion berechnet, findet man hier: Ableitungsregeln) gibt die Steigung der Funktion an und lautet \(f'(x)=x^2-3x+2\). Die faktorisierte Form der Ableitungsfunktion (kann man durch Nullsetzen \(=(x-1)\cdot (x-2)=0\) und Lösen der Gleichung ermitteln) lautet \(f'(x)=(x-1)\cdot (x-2)\). Multipliziert man die Klammern aus, so erhält man wiederum die allgemeine Form \(f'(x)=x^2-3x+2\).

Um zu untersuchen, bei welchen Stellen die Ableitungsfunktion das Vorzeichen wechselt, betrachten wir die faktorisierte Form \(f'(x)=(x-\color{blue}{1})\cdot (x-\color{blue}{2})\). Dabei haben wir die Stellen \(x_1=\color{blue}{1}\) und \(x_2=\color{blue}{2}\) hervorgehoben. Warum?

Der Term \((x-\color{blue}{1})\) ist für alle \(x\), die kleiner sind als \(\color{blue}{1}\), negativ und hat damit ein negatives Vorzeichen.
Der Term \((x-\color{blue}{2})\) ist für alle \(x\), die kleiner sind als \(\color{blue}{2}\), negativ und hat damit ein negatives Vorzeichen.

Jetzt überlegen wir uns, wie das Vorzeichen für die gesamte Ableitungsfunktion aussieht.

Zuerst für alle \(x < 1\): Da beide Terme, \((x-1)\) und \((x-2)\), negativ sind, hat man 'Minus mal Minus', da sie miteinander multipliziert werden. Also ein positives Vorzeichen!
Für alle \(1 < x < 2\): Da der Terme \((x-1)\) positiv ist und der Term \((x-2)\) negativ ist, hat man 'Plus mal Minus'. Also ein negatives Vorzeichen!
Für alle \(x > 2\): Da beide Terme, \((x-1)\) und \((x-2)\), positiv sind, hat man 'Plus mal Plus'. Also ein positives Vorzeichen!

Damit sind bei \(x=1\) und bei \(x=2\) jeweils Monotoniewechsel gegeben. Das ist auch in der Grafik unterhalb ersichtlich, in der der Funktionsgraph der Funktion dargestellt ist.

Monotoniewechsel Beispiel — Figur zum vierten Beispiel.

Zu den interaktiven Aufgaben → Monotonie Definition - Übungsaufgaben

Zu den interaktiven Aufgaben → Monotoniewechsel - Übungsaufgaben

Weiterführende Artikel: