Funktionsgraph

Der Graph bzw. Funktionsgraph einer Funktion ist die grafische Darstellung der Funktion.

Dabei zeichnet man zwei reelle Skalen ein, die horizontale x-Achse (Abszissenachse) und die vertikale y-Achse (Ordinatenachse). Die Kurve, die die Funktion darstellt, bringt Werte von der x-Achse und der y-Achse in Verbindung. Jedem Wert auf der x-Achse wird ein Wert auf der y-Achse zugewiesen gemäß der Abbildungsvorschrift \(x\mapsto y=f(x)\). Also, nimmt man einen Wert \(x\), so ist der zugewiesene Wert \(y\) durch die Vorschrift \(f(x)\) gegeben.

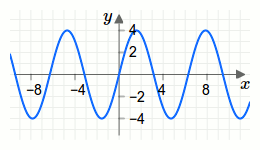
Die Funktion \[f: \mathbb{R}\rightarrow \mathbb{R}\] \[x\mapsto f(x)=4\cdot \sin (x)\] hat den Graph der in der nächsten Grafik dargestellt ist.

Funktionsgraph aus Wertetabelle erstellen

Wir sehen uns nun an, wie man aus einer gegebenen Funktion einen Funktionsgraphen erstellen kann. Dazu erstellt man üblicherweise eine Wertetabelle. Wir werden das Ganze anhand eines Beispiels durchgehen.

Es ist die Funktion\[f: \mathbb{R}\rightarrow \mathbb{R}\] \[x\mapsto y=f(x)=3+x\] gegeben. Erstelle eine Wertetabelle!

Wir schreiben auf: \[\begin{array}{c|c} x & y \\ \hline 1 & \\ 2 & \\ 3 & \\ 4 & \\ 5 & \end{array}\] Dabei kann man anstatt der Werte \(1;2;3;4;5\) beliebige andere Zahlen nehmen und auch beliebig viele. Nun müssen wir herausfinden wie die fehlenden \(y\)-Werte der Wertetabelle lauten. Es ist doch \(y=f(x)\). \[\begin{array}{c|c} x & y \\ \hline {\color{red}1} & f({\color{red}1}) \\ {\color{red}2} & f({\color{red}2}) \\ {\color{red}3} & f({\color{red}3}) \\ {\color{red}4} & f({\color{red}4}) \\ {\color{red}5} & f({\color{red}5}) \end{array}\] Wir setzen in die Funktion ein: \[\begin{array}{rl}f({\color{red}1})&=3+{\color{red}1}=4\\ f({\color{red}2})&=3+{\color{red}2}=5\\ f({\color{red}3})&=3+{\color{red}3}=6\\ f({\color{red}4})&=3+{\color{red}4}=7\\ f({\color{red}5})&=3+{\color{red}5}=8 \end{array}\] \[\begin{array}{c|c} x & y \\ \hline 1 & 4\\ 2 & 5\\ 3 & 6\\ 4 & 7\\ 5 & 8 \end{array}\] In der ersten Spalte sind die \(x\)-Koordinaten bzw. Komponenten gegeben. In der zweiten Spalte die \(y\)-Koordinaten.

Übrigens nennt man zwei zusammengehörige \(x\)- und \(y\)-Werte auch Wertepaar. Ein Punkt in einer Ebene ist durch \(P=\left(\begin{array}{c}x\\y\end{array}\right)\) gegeben. Die Tabelle vom ersten Beispiel listet fünf Punkte auf, die dieselbe Funktion beschreiben. Tendenziell gilt: Je mehr Punkte gegeben sind, desto genauer kann die Funktion gezeichnet werden.

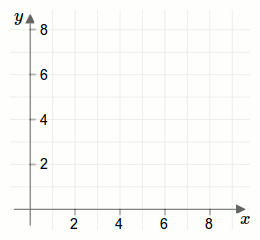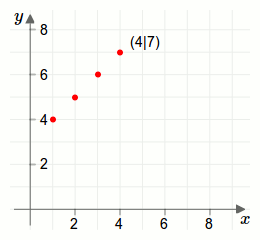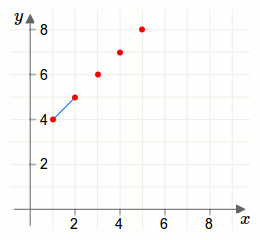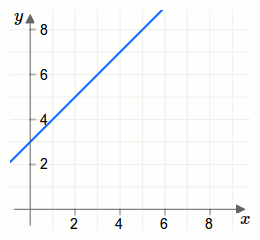
Erstelle den Funktionsgraphen der Funktion \(f(x)=3+x\) !

Wir zeichnen nun den ersten Punkt \(P=\begin{pmatrix}1\\4\end{pmatrix}\) der Tabelle auf der Ebene ein. Dann den zweiten Punkt \(P=\begin{pmatrix}2\\5\end{pmatrix}\). Und so weiter.

Verbindet man nun die Punkte mit Linien, so kann man den Funktionsgraph erkennen.

Diese Vorgehensweise ist in der folgenden Animation dargestellt.

Erstellung eines Funktionsgraphen aus einer Wertetabelle

Zu den interaktiven Aufgaben → Funktionsgraph - Übungsaufgaben

Weiterführende Artikel: