Vektor bzw. Zahlentupel
Ein Zahlentupel bzw. Vektor ist eine Auflistung von Zahlen, bei der die Reihenfolge der Elemente festgelegt ist. Für die Darstellung eines Zahlentupels verwendet man gewöhnliche runde Klammern. Man kann ein Zahlentupel horizontal oder vertikal aufschreiben.Der Ausdruck \(\begin{pmatrix}2\\5\\3\end{pmatrix}\) ist ein Zahlentupel in vertikaler Schreibweise. Die horizontale Schreibweise dazu lautet \(\left(2;5;3\right)\).
Es werden auch andere Trennzeichen bei der horizontalen Schreibweise verwendet, etwa wie im folgenden Beispiel.
\(\left(2|5|3\right)\).
Wichtig ist der Unterschied zu Mengen! Eine Menge ist eine Auflistung bei der die Reihenfolge der Elemente keine Rolle spielt. Bei der Darstellung von Mengen werden geschwungene Klammern verwendet.Es gibt verschiedene Verwendungsmöglichkeiten für einen Vektor. Die wichtigsten Möglichkeiten sind:
- Ein Vektor kann einen Punkt (auf einer Ebene oder im Raum) darstellen.
- Ein Vektor kann einen Pfeil/Zeiger darstellen, der eine Richtung und eine Länge hat.
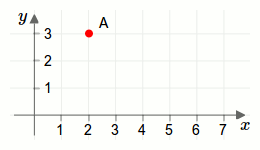In der Grafik wurde ein Punkt in einer Ebene eingezeichnet. Zur besseren Orientierung haben wir in der Grafik zwei Skalen eingezeichnet. Eine horizontale und eine vertikale Skala. Damit können wir nun jeden Punkt auf der Ebene derart beschreiben, dass die Lage des Punktes klar und eindeutig ist. Wir benötigen also um einen Punkt in einer Ebene zu beschreiben zwei reelle Zahlen. Eine Zahl, die angibt wie weit links/rechts der Punkt liegt und eine Zahl wie weit oben/unten der Punkt liegt, und zwar ausgehend von der Null auf den jeweiligen Skalen. Das System mit den Skalen nennt man übrigens Koordinatensystem.
Die zwei Zahlen, die den Punkt \(\vec{A}\) beschreiben, werden in einem sogenannten Zahlentupel bzw. Vektor dargestellt. Der Punkt \(\vec{A}\) in der Grafik kann also durch folgendem Vektor beschrieben werden:
\[\vec{A}=\begin{pmatrix}2\\3\end{pmatrix}\]
Die einzelnen Einträge eines Vektors nennt man Komponenten.
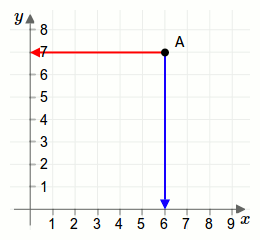
Wir betrachten den Punkt \(\vec{A}\), der in der nächsten Grafik eingezeichnet ist. Der Punkt bzw. Vektor \(\vec{A}=\begin{pmatrix}6\\7\end{pmatrix}\) hat zwei Komponenten, die erste Komponente lautet \(\color{blue}{6}\) und die zweite lautet \(\color{red}{7}\).
Dafür sehen wir uns die vertikale und horizontale Linien an, die vom Punkt \(\vec{A}\) zu den Achsen gehen.
Dort wo die Linien die Achsen berühren kann man die Komponenten ablesen.
Ein Pfeil bzw. Zeiger ist eine grafische Darstellung eines Vektors. Die Pfeilspitze zeigt in die Richtung des Vektors.
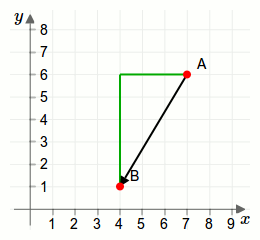
Wir betrachten den Pfeil, der in der Grafik zuvor eingezeichnet ist. Er zeigt vom Punkt \(\vec{A}\) zum Punkt \(\vec{B}\). Wir versuchen nun den entsprechenden Vektor hinzuschreiben. Dazu haben wir zwei grüne Hilfslinien eingezeichnet. Diese helfen uns dabei die Komponenten zu bestimmen. Zuerst bestimmen wir die Länge der horizontalen Hilfslinie: Sie ist genau 3 Einheiten (Kästchen) lang. Die vertikale Hilfslinie ist genau 5 Einheiten lang. Achtung, wir haben uns jetzt jeweils bei den Skalen von größeren Werten zu kleineren bewegt. Das muss natürlich nicht immer so sein. (Etwa wenn wir den Pfeil umgekehrt gezeichnet hätten, also von \(\vec{B}\) nach \(\vec{A}\).) Da wir auf der Skala von größeren zu kleineren Werten gegangen sind, sind die Komponenten im Vektor negativ!
\[\vec{B}-\vec{A}=\begin{pmatrix}-3\\-5\end{pmatrix}\]
Dieser Vektor gibt also an, wie wir von Punkt \(\vec{A}\) nach Punkt \(\vec{B}\) kommen. Ein Minus bedeutet also, dass man auf der Skala hinab zählt und nicht hinauf.
Zu den interaktiven Aufgaben → Vektoren - Übungsaufgaben
Weiterführende Artikel:
Hat alles, was man braucht: Taschenrechner CASIO FX-991DE X *
Die mit Sternchen (*) gekennzeichneten Verweise sind sogenannte Provisions-Links. Für dich entstehen dabei keine Nachteile!