Optische Linsen

In diesem Artikel werden optische Linsen betrachtet und die Linsengleichung angegeben und erklärt.

Sammellinsen und Zerstreuungslinsen

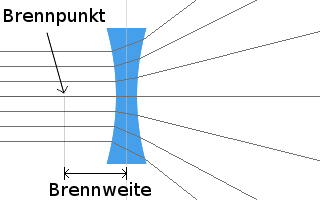
Optische Linsen werden verwendet um Licht entweder zu bündeln oder zu zerstreuen. Man kann dadurch Gegenstände optisch vergrößern oder verkleinern. Linsen, die Licht bündeln, nennt man Sammellinsen und Linsen, die Licht streuen, nennt man Zerstreuungslinsen.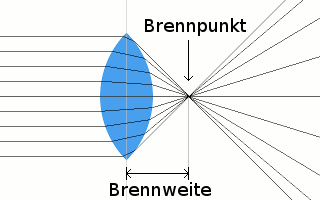

Grafik bikonvexe Sammellinse — Eine (bikonvexe) Sammellinse bündelt aufgrund von Lichtbrechung Licht im (rechten) Brennpunkt.

Grafik bikonkave Zerstreuungslinse — Eine (bikonkave) Zerstreuungslinse zerstreut aufgrund von Lichtbrechung Licht. Dabei zeigen die Lichtstrahlen nach der Streuung in jene Richtungen, als ob sie vom (linken) Brennpunkt kommen würden.

Linsengleichung bzw. Abbildungsgleichung

Linsen werden dazu verwendet, um Gegenstände optisch zu vergrößern oder zu verkleinern. Die wichtigste Größe einer Linse ist ihre Brennweite. Als Symbol verwendet man üblicherweise \(f\) (f wie 'Fokus' oder 'focal length'). Die Brennweite ist der Abstand von der Linsenachse zu einem der Brennpunkte (links oder rechts von der Linse). Bildet man einen Gegenstand durch eine Linse ab, so gibt es zwei weitere Größen, die Gegenstandsweite \(g\) und die Bildweite \(b\), die von der Position des Gegenstandes zur Linse und von der Brennweite abhängig sind.
Die Vergrößerung einer Linse ist durch \(A=\frac{b}{g}\) gegeben.

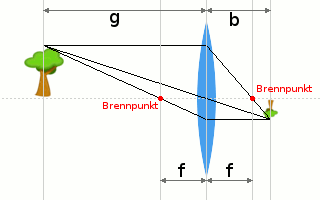
Darstellung von Brennweite, Gegenstandsweite und Bildweite.

Die Linsengleichung (bzw. auch Abbildungsgleichung genannt) gibt den Zusammenhang zwischen Brennweite \(f\), Gegenstandsweite \(g\) und Bildweite \(b\) einer Linse. \[\frac{1}{b}+\frac{1}{g}=\frac{1}{f}\]

Aufgaben mit Lösungen

Ein Gegenstand soll durch eine Linse mit einer gegebenen Brennweite \(f\) mit einer bestimmten Vergrößerung \(A\) erscheinen. Wie groß müssen dann die Gegenstandsweite und die Bildweite sein?

Es ist \(f\) und \(A=\frac{b}{g}\) gegeben und \(b\) sowie \(g\) gesucht.
Wir formen die Linsengleichung um: \[\frac{1}{b}+\frac{1}{g}=\frac{1}{f}\qquad \color{gray}{|\cdot b}\] \[\frac{b}{b}+\frac{b}{g}=\frac{b}{f}\] \[1+A=\frac{b}{f}\qquad \color{gray}{|\cdot f}\] \[f\cdot (1+A)=b\] Die Bildweite kann also durch \(b=f\cdot (1+A)\) berechnet werden.

Wir formen die Linsengleichung nochmals um: \[\frac{1}{b}+\frac{1}{g}=\frac{1}{f}\qquad \color{gray}{|\cdot g}\] \[\frac{g}{b}+\frac{g}{g}=\frac{g}{f}\] \[\frac{1}{A}+1=\frac{g}{f}\qquad \color{gray}{|\cdot f}\] \[f\cdot (\frac{1}{A}+1)=g\] Die Gegenstandsweite kann also durch \(g=f\cdot (\frac{1}{A}+1)\) berechnet werden.

Zu den interaktiven Aufgaben → Optische Linsen - Übungsaufgaben