MathematikMathematik

Eine Gerade in einer Ebene kann durch zwei voneinander verschiedenen Punkten, die beide auf der Geraden liegen, dargestellt werden. Diese Darstellung nennt man Parameterdarstellung einer Geraden.
Parameterdarstellung einer Geradengleichung
Man geht also von zwei voneinander verschiedenen Punkten \(\vec{A}\) und \(\vec{B}\) aus, die auf der entsprechenden Geraden liegen. Wir stellen fest: Addiert man zu einem beliebigen Punkt, der auf der Geraden liegt, die Differenz der beiden Vektoren \((\vec{B}-\vec{A})\), so erhält man wieder einen Punkt der auf der Geraden liegt. Addiert man \(t\cdot (\vec{B}-\vec{A})\), wobei \(t\) eine beliebige reelle Zahl ist, so bleibt man weiterhin auf der Geraden.
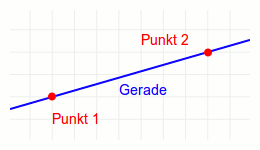
Wir folgern: Man kann einen beliebigen Punkt auf einer Geraden mittels eines Parameters und zwei Punkten beschreiben.
Die Parameterdarstellung einer Geraden, welche durch zwei voneinander verschiedenen Punkte \(\vec{A}\) und \(\vec{B}\) verläuft, lautet \[\vec{P}=\vec{A}+t\cdot (\vec{B}-\vec{A})\] Schreibt man die Vektoren mit ihren Komponenten an, so ergibt sich \[\begin{pmatrix}x\\y\end{pmatrix}=\begin{pmatrix}a_1\\a_2\end{pmatrix}+t\cdot\begin{pmatrix}b_1-a_1\\b_2-a_2\end{pmatrix}\]

Beispiele und Aufgaben mit Lösungen

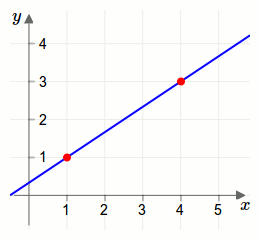
In der nächsten Grafik ist \(\vec{A}=\begin{pmatrix}1\\1\end{pmatrix}\) und \(\vec{B}-\vec{A}=\begin{pmatrix}4\\3\end{pmatrix}-\begin{pmatrix}1\\1\end{pmatrix}=\begin{pmatrix}4-1\\3-1\end{pmatrix}=\begin{pmatrix}3\\2\end{pmatrix}\).
Parameterdarstellung einer Geradengleichung
Stelle eine Parameterdarstellung der Gerade auf, die durch die beiden Punkte \(\vec{A}=\begin{pmatrix}3\\2\end{pmatrix}\) und \(\vec{B}=\begin{pmatrix}5\\6\end{pmatrix}\) geht!
Wir berechnen \(\overrightarrow{AB}=\vec{B}-\vec{A}=\begin{pmatrix}5\\6\end{pmatrix}-\begin{pmatrix}3\\2\end{pmatrix}=\begin{pmatrix}5-3\\6-2\end{pmatrix}=\begin{pmatrix}2\\4\end{pmatrix}\).
Eine Parameterdarstellung der Gerade lautet \[\vec{P}=\vec{A}+t\cdot \overrightarrow{AB}.\] \[\begin{pmatrix}x\\y\end{pmatrix}=\begin{pmatrix}3\\2\end{pmatrix}+t\cdot \begin{pmatrix}2\\4\end{pmatrix}\]
Es ist eine Gerade gegeben: \[\begin{pmatrix}x\\y\end{pmatrix}=\begin{pmatrix}1\\0\end{pmatrix}+t\cdot \begin{pmatrix}-2\\3\end{pmatrix}.\] Liegt der Punkt \(\begin{pmatrix}-7\\9\end{pmatrix}\) auf der Gerade?
Wir setzen den Punkt in die Geradengleichung ein. \[\begin{pmatrix}-7\\9\end{pmatrix}=\begin{pmatrix}1\\0\end{pmatrix}+t\cdot \begin{pmatrix}-2\\3\end{pmatrix}\] Wir erhalten zwei Gleichungen: \[-7=1+t\cdot (-2)\] und \[9=0+t\cdot 3.\] Wir lösen die erste Gleichung nach \(t\) auf. \[-7=1+t\cdot (-2)\qquad\color{gray}{|-1}\] \[-8=-2t\qquad\color{gray}{|:(-2)}\] \[4=t\] Wir setzen \(t=4\) in die zweite Gleichung ein. \[9=0+4\cdot 3\] \[9=12\] Das ist falsch! Damit liegt der Punkt nicht auf der Gerade.
Weiterführende Artikel: