Periodizität einer Funktion

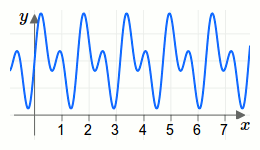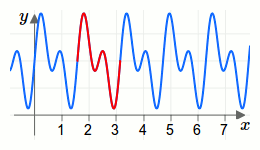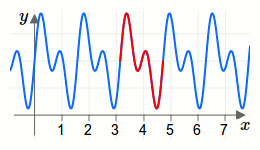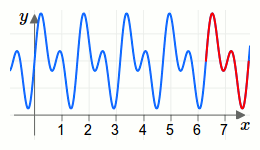
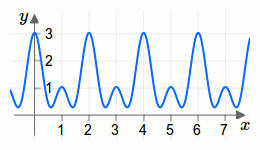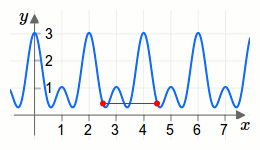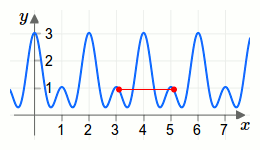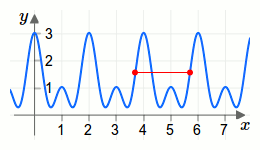
Eine mathematische Funktion nennt man periodisch, wenn es eine Konstante \(c\) gibt, sodass für die Funktion \(f\) die Beziehung \(f(x+c)=f(x)\) gilt. Die Konstante \(c\) nennt man dann Periodizität. Den Kehrwert \(\frac{1}{c}\) der Periodizität nennt man Frequenz.
In der folgenden Animation wird die Periodizität einer periodischen Funktion visualisiert.

Animation der Periodizität einer periodischen Funktion

Die grundlegende Eigenschaft \(f(x+c)=f(x)\) einer periodischen Funktion ist in der nächsten Animation durch dargestellt. Dabei stellt die rote Linie, dessen Länge stets gleich bleibt die Konstante \(c\) dar.

Darstellung der Periodizität einer Funktion

Beispiele und Aufgaben mit Lösungen

Die Sinusfunktion ist periodisch und hat die Periodizität \(2\pi\). Damit gilt \(\sin(x+2\pi)=\sin(x)\) und zwar für jedes beliebige \(x\in\mathbb{R}\).

Bemerkung: \(2\pi\) ist in Radiant gegeben und entspricht \(360^{\circ}\).

Es ist \(f\) eine periodische Funktion mit der Periodizität \(4\). Damit gilt \(f(x+4)=f(x)\). Was ist dann \(f(x+8)\) ?

Es ist \(f(x+4)=f(x)\). Wir ersetzen nun \(x\rightarrow x+4\). Damit ist \(f(x+4+4)=f(x+4)\) und weiter \(f(x+8)=f(x+4)\).
Es gilt \(f(x+4)=f(x)\) also ist \(f(x+8)=f(x)\).

Es sind \(f\) und \(g\) zwei periodische Funktionen. Es gilt \(f(x+2)=f(x)\) und \(g(x+3)=g(x)\). Ist die Funktion \(h=f+g\) auch periodisch?

Es gilt \(h(x+6)=f(x+6)+g(x+6)=f(x)+g(x)=h(x)\). Also ist \(h\) auch periodisch.

Es sind \(f\) und \(g\) zwei periodische Funktionen. Es gilt \(f(x+2)=f(x)\) und \(g(x+5)=g(x)\). Ist die Funktion \(h=f\cdot g\) auch periodisch?

Es gilt \(h(x+10)=f(x+10)\cdot g(x+10)=f(x)\cdot g(x)=h(x)\).
Also ist \(h\) auch periodisch.

Wie lautet die Periodizität der Sinusfunktion \(f(x)=\sin (3x)\) ?

Wir setzen \(3x=2\pi\) und formen um zu \(x=\frac{2\pi}{3}\).
Die Periodizität lautet \(\frac{2\pi}{3}\).

Wie lautet die Periodizität der Kosinusfunktion \(f(x)=\cos (4x+1)\) ?

Wir setzen \(4x=2\pi\) und formen um zu \(x=\frac{2\pi}{4}\).
Die Periodizität lautet \(\frac{\pi}{2}\).

Die Funktion \(f(x)=\sin (x^2)\) ist nicht periodisch!

Wie lautet die Periodizität der Kosinusfunktion \(f(x)=\cos (\pi\cdot x)\) ?

Wir setzen \(\pi\cdot x=2\pi\) und formen um zu \(x=\frac{2\pi}{\pi}=2\).
Die Periodizität lautet \(2\).

Zu den interaktiven Aufgaben → Periodizität und Frequenz einer Funktion - Übungsaufgaben