Sinusfunktion, Kosinusfunktion und Tangensfunktion
Winkelfunktionen wie etwa die Sinusfunktion \[f(x)=\sin (x)\] oder die Kosinusfunktion \[f(x)=\cos (x)\] haben eine typische Eigenschaft, sie sind periodisch. Eine weitere Winkelfunktion ist die Tangensfunktion \(f(x)=\tan (x)=\frac{\sin (x)}{\cos (x)}\), die durch die Sinusfunktion und durch die Kosinusfunktion dargestellt werden kann.In der Grafik unterhalb ist der Funktionsgraph der Winkelfunktion \(f(x)=2\cdot \sin (2x)\) dargestellt.
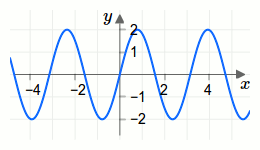
Zu den interaktiven Aufgaben → Winkelfunktionen - Übungsaufgaben
Parameter der Sinusfunktion und der Kosinusfunktion
Die allgemeine Sinusfunktion lautet \[f(x)=a\cdot \sin (b\cdot x + c)+d\] Ganz ähnlich lautet die allgemeine Kosinusfunktion bzw. Cosinusfunktion, und zwar \[f(x)=a\cdot \cos (b\cdot x + c)+d\] Bei beiden Funktionen haben die Parameter \(a, b, c\) und \(d\) welche beliebige reelle Zahlen sein können.Amplitude
Variiert bzw. verändert man den Parameter \(a\), so lässt sich die allgemeine Sinusfunktion bzw. Kosinusfunktion stauchen oder strecken bzw. dehnen oder zusammenziehen, und zwar entlang der y-Achse. In der folgenden interaktiven Grafik sehen wir den Graph der Funktion \(f(x)=a\cdot\sin (x)\). Verschiebe den Regler um die Amplitude zu variieren und die Bedeutung dieses Parameters kennen zu lernen!Periodizität
Variiert bzw. verändert man den Parameter \(b\), so lässt sich die allgemeine Sinusfunktion \(f(x)=a\cdot \sin (b\cdot x + c)\) stauchen oder strecken bzw. dehnen oder zusammenziehen, und zwar entlang der x-Achse. In der nächsten interaktiven Grafik ist der Funktionsgraph von \(f(x)=\sin (b\cdot x)\) dargestellt.Phase
Variiert bzw. verändert man den Parameter \(c\), so lässt sich die allgemeine Sinusfunktion \(f(x)=a\cdot \sin (b\cdot x + c)\) entlang der x-Achse verschieben. In der folgenden interaktiven Grafik sehen wir den Graph der Funktion \(f(x)=\sin (x + c)\).Additive Konstante
Variiert bzw. verändert man den Parameter \(d\), so lässt sich die allgemeine Sinusfunktion \(f(x)=a\cdot \sin (b\cdot x + c)+d\) entlang der y-Achse verschieben. In der nächsten interaktiven Grafik sehen wir den Graph der Funktion \(f(x)=\sin (x)+d\). Verschiebe den Regler um den Parameter zu variieren und die Bedeutung des Parameters kennen zu lernen!Zu den interaktiven Aufgaben → Sinusfunktion und ihre Parameter - Übungsaufgaben
Zu den interaktiven Aufgaben → Kosinusfunktion und ihre Parameter - Übungsaufgaben
Zusammenhang Sinusfunktion und Kosinusfunktion
Der Zusammenhang der Sinusfunktion und der Kosinusfunktion ist über die Phase gegeben. Es gilt \[\cos (x)=\sin (x+\frac{\pi}{2})\] Dabei ist \(\pi\approx 3.141592654\) die Kreiszahl Pi. In der folgenden interaktiven Grafik sind die Funktionsgraphen von \(f_1(x)=\cos (x)\) (grüner Funktionsgraph) und \(f_2(x)=\sin (x+c)\) (blauer Funktionsgraph) eingezeichnet. Bei \(c=\frac{\pi}{2}\approx 1{,}57\) sind beide Funktionen gleich! Verschiebe den Regler für den Parameter \(c\) derart, dass die beiden Funktionen übereinander liegen! Wie lautet dann der Parameter \(c\)?Zu den interaktiven Aufgaben → Zusammenhang Sinusfunktion und Kosinusfunktion - Übungsaufgaben
Hat alles, was man braucht: Taschenrechner CASIO FX-991DE X *
Die mit Sternchen (*) gekennzeichneten Verweise sind sogenannte Provisions-Links. Für dich entstehen dabei keine Nachteile!