Reflexion von Licht
In diesem Artikel wird die Reflexion, das Reflexionsgesetz und die Totalreflexion angegeben und erklärt.
Trifft Licht auf eine Grenzfläche zwischen zwei verschiedenen Medien (wie Glas, Wasser oder Luft), so wird ein Teil des Lichts reflektiert. Diesen Vorgang nennt man Reflexion. Der andere Teil des Lichts geht durch das zweite Medium und wird dabei meist gebrochen.
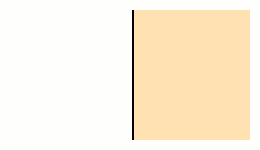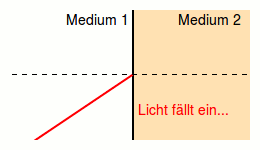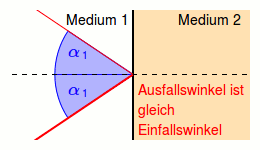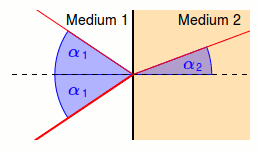
Wie lautet das Reflexionsgesetz?
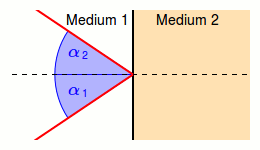
Trifft Licht unter einem Einfallswinkel auf eine Grenzfläche zweier verschiedener Medien, so gilt für den Ausfallswinkel des reflektierten Teils des Lichts, dass Einfallswinkel und Ausfallswinkel gleich groß sind.
\[\alpha _1=\alpha _2\]
Der Einfallswinkel \(\alpha_1\) und der Ausfallswinkel \(\alpha_2\) werden jeweils zum Lot hin gemessen (senkrecht zur Oberfläche).
Was ist Totalreflexion?
In manchen Situationen kann es vorkommen, dass das gesamte Licht reflektiert wird. Man spricht dann von Totalreflexion. In solchen Fällen gibt es einen kritischen Einfallswinkel, der mit dem Brechungsgesetz \[n_1\cdot \sin (\alpha_1)=n_2\cdot \sin (\alpha_2)\] hergeleitet werden kann. Dabei sind \(n_1\) und \(n_2\) die Brechungsindizes der beiden Medien. Der kritische Einfallswinkel \(\alpha_k\) ist so definiert, dass der gebrochene Winkel \(\alpha_2=90^{\circ}\). \[n_1\cdot \sin (\alpha_k)=n_2\cdot \sin (90^{\circ})\] \[n_1\cdot \sin (\alpha_k)=n_2\cdot 1\] \[\sin (\alpha_k)=\frac{n_2}{n_1}\] \[\alpha_k=\arcsin (\frac{n_2}{n_1})\] Der Arcussinus darf nur auf Zahlen zwischen -1 und +1 angewendet werden. Damit kann eine Totalreflexion nur zwischen zwei Medien vorkommen, wenn \(\frac{n_2}{n_1}\leq 1\).Bei Glasfaserkabeln nutzt man die Totalreflexion des Lichts aus.
Die Brechzahl von Luft ist ungefähr 1, die Brechzahl von gewöhnlichem Glas ist in etwa 1,5. Wir schreiben \(n_1=1{,}5\) und \(n_2=1{,}0\) für Licht, dass in Glas auf eine Glas-Luft-Grenzfläche trifft. Der kritische Winkel für Licht innerhalb eines Glasfaserkabels ist durch \[\alpha_k=\arcsin (\frac{1}{1{,}5})\approx 41{,}8^{\circ}\] gegeben. Ist der Winkel also größer als \(41{,}8^{\circ}\) so bleibt das Licht innerhalb des Glasfaserkabels und tritt erst an dessen Ende hinaus - aber nur wenn die Glasfaserkabel von Luft umgeben sind. Taucht man sie beispielsweise in Wasser, dann ändert sich der kritische Einfallswinkel. (Handelsübliche Glasfasern sind komplexer aufgebaut als hier in dem Beispiel und bestehen aus einem Kern und mehreren Mänteln. Das Grundprinzip ist jedoch in diesem Beispiel gegeben.)
Zu den interaktiven Aufgaben → Reflexion - Übungsaufgaben
Hat alles, was man braucht: Taschenrechner CASIO FX-991DE X *
Die mit Sternchen (*) gekennzeichneten Verweise sind sogenannte Provisions-Links. Für dich entstehen dabei keine Nachteile!