Wahrscheinlichkeitsverteilung
Eine Wahrscheinlichkeitsverteilung (bzw. Verteilung) beschreibt die Wahrscheinlichkeiten \(p\) der möglichen Werte einer Zufallsvariable \(x\). Allgemein kann eine Wahrscheinlichkeitsverteilung als Funktion betrachtet werden.Aufgaben mit Lösungen
Sei \(x\in\{1;2;3;4;5;6\}\) die Augenzahl, die mit einem gewöhnlichen fairen Würfel gewürfelt wird. Wie lautet die Wahrscheinlichkeitsverteilung?
Dann ist \(p(x)=\frac{1}{6}\) die Wahrscheinlichkeit die Augenzahl \(x\) zu würfeln. Die (konstante) Funktion \(p(x)=\frac{1}{6}\) beschreibt also die Wahrscheinlichkeitsverteilung dieses Vorgangs.
Jemand würfelt zweimal hintereinander mit einem fairen Würfel und addiert anschließend die beiden gewürfelten Augenzahlen. Wie wahrscheinlich ist es die Summe 12 zu würfeln? Wie wahrscheinlich ist es die Summe 10 zu würfeln?
Um die Augenzahlsumme 2 zu würfeln gibt es nur eine Kombination (⚀+⚀).
Um die Augenzahlsumme 3 zu würfeln gibt es zwei Kombinationen (⚀+⚁, ⚁+⚀).
Um die Augenzahlsumme 4 zu würfeln gibt es drei Kombinationen (⚀+⚂, ⚁+⚁, ⚂+⚀).
Um die Augenzahlsumme 5 zu würfeln gibt es vier Kombinationen (⚀+⚃, ⚁+⚂, ⚂+⚁, ⚃+⚀).
Um die Augenzahlsumme 6 zu würfeln gibt es fünf Kombinationen (⚀+⚄, ⚁+⚃, ⚂+⚂, ⚃+⚁, ⚄+⚀).
Um die Augenzahlsumme 7 zu würfeln gibt es sechs Kombinationen (⚀+⚅, ⚁+⚄, ⚂+⚃, ⚃+⚂, ⚄+⚁, ⚅+⚀).
Um die Augenzahlsumme 8 zu würfeln gibt es fünf Kombinationen (⚁+⚅, ⚂+⚄, ⚃+⚃, ⚄+⚂, ⚅+⚁).
Um die Augenzahlsumme 9 zu würfeln gibt es vier Kombinationen (⚂+⚅, ⚃+⚄, ⚄+⚃, ⚅+⚂).
Um die Augenzahlsumme 10 zu würfeln gibt es drei Kombinationen (⚃+⚅, ⚄+⚄, ⚅+⚃).
Um die Augenzahlsumme 11 zu würfeln gibt es zwei Kombinationen (⚄+⚅, ⚅+⚄).
Um die Augenzahlsumme 12 zu würfeln gibt es eine Kombination (⚅+⚅).
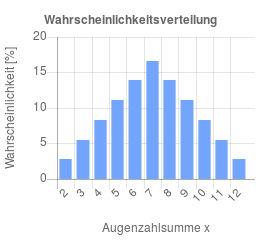
Um die Wahrscheinlichkeiten für eine bestimmte Augenzahlsumme zu berechnen muss die Anzahl an Kombinationen durch 36 dividiert werden, da es insgesamt 36 Kombinationen gibt. Die Wahrscheinlichkeit die Augenzahlsumme 12 zu Würfeln liegt damit bei 2,78%. In der nächsten Grafik wird die Wahrscheinlichkeitsverteilung mittels eines Säulendiagramm dargestellt.
Um die Augenzahlsumme 3 zu würfeln gibt es zwei Kombinationen (⚀+⚁, ⚁+⚀).
Um die Augenzahlsumme 4 zu würfeln gibt es drei Kombinationen (⚀+⚂, ⚁+⚁, ⚂+⚀).
Um die Augenzahlsumme 5 zu würfeln gibt es vier Kombinationen (⚀+⚃, ⚁+⚂, ⚂+⚁, ⚃+⚀).
Um die Augenzahlsumme 6 zu würfeln gibt es fünf Kombinationen (⚀+⚄, ⚁+⚃, ⚂+⚂, ⚃+⚁, ⚄+⚀).
Um die Augenzahlsumme 7 zu würfeln gibt es sechs Kombinationen (⚀+⚅, ⚁+⚄, ⚂+⚃, ⚃+⚂, ⚄+⚁, ⚅+⚀).
Um die Augenzahlsumme 8 zu würfeln gibt es fünf Kombinationen (⚁+⚅, ⚂+⚄, ⚃+⚃, ⚄+⚂, ⚅+⚁).
Um die Augenzahlsumme 9 zu würfeln gibt es vier Kombinationen (⚂+⚅, ⚃+⚄, ⚄+⚃, ⚅+⚂).
Um die Augenzahlsumme 10 zu würfeln gibt es drei Kombinationen (⚃+⚅, ⚄+⚄, ⚅+⚃).
Um die Augenzahlsumme 11 zu würfeln gibt es zwei Kombinationen (⚄+⚅, ⚅+⚄).
Um die Augenzahlsumme 12 zu würfeln gibt es eine Kombination (⚅+⚅).
Um die Wahrscheinlichkeiten für eine bestimmte Augenzahlsumme zu berechnen muss die Anzahl an Kombinationen durch 36 dividiert werden, da es insgesamt 36 Kombinationen gibt. Die Wahrscheinlichkeit die Augenzahlsumme 12 zu Würfeln liegt damit bei 2,78%. In der nächsten Grafik wird die Wahrscheinlichkeitsverteilung mittels eines Säulendiagramm dargestellt.
Zu den interaktiven Aufgaben → Wahrscheinlichkeitsverteilung - Übungsaufgaben
Weiterführende Artikel:
Hat alles, was man braucht: Taschenrechner CASIO FX-991DE X *
Die mit Sternchen (*) gekennzeichneten Verweise sind sogenannte Provisions-Links. Für dich entstehen dabei keine Nachteile!