Wendepunkt einer differenzierbaren Funktion berechnen
In diesem Artikel wird gezeigt wie man einen Wendepunkt oder einen Terrassenpunkt einer dreimal differenzierbaren Funktion berechnen kann.
Die Wendepunkte einer dreimal differenzierbaren Funktion können durch die zweite und dritte Ableitungsfunktion berechnet werden.
An der Stelle \(x_0\) einer dreimal differenzierbaren Funktion \(f\) liegt ein Wendepunkt vor, wenn \(f''(x_0) = 0\) und \(f'''(x_0) \neq 0\) sind.
Die Wendepunkte einer dreimal differenzierbaren Funktion können durch folgende Schritte berechnet werden:
- Berechnen der zweiten Ableitungsfunktion \(f''\).
- Ermittlen der Nullstellen \(x_0\) der zweiten Ableitungsfunktion: \(f''(x_0)=0\).
- Berechnen der dritten Ableitungsfunktion \(f''\).
- Einsetzen der Nullstellen in die dritte Ableitungsfunktion:
- Ist \(f'''(x_0) \neq 0\), so ist ein Wendepunkt gegeben.
- Ist \(f'''(x_0)=0\), so sind weitere Untersuchungen notwendig (Es kann ein Wendepunkt gegeben sein).
Sei \(f(x)=x+(x-1)^3\). Die Ableitungsfunktion lautet \(f'(x)=1+3(x-1)^2\). Die Ableitungsfunktion der Ableitungsfunktion (=zweite Ableitungsfunktion) lautet \(f''(x)=6(x-1)\). Die dritte Ableitungsfunktion lautet \(f'''(x)=6\).
Wir suchen nun die Nullstellen der zweiten Ableitungsfunktion. Dazu betrachten wir \(f''(x_0)=6(x_0-1)=0\). Wir formen um zu \(x_0-1=0\). Die Lösung der Gleichung lautet \(x_0=1\).
An der Stelle \({\color{green}{x_0=1}}\) lautet die dritte Ableitung \(f'''(x_0)=6\neq 0\). An der Stelle \({\color{green}{x_0=1}}\) hat die Funktion daher einen Wendepunkt.
Der Funktionsgraph der Funktion \(f\) sowie der Wendepunkt sind in der nächsten Grafik dargestellt.
Wir suchen nun die Nullstellen der zweiten Ableitungsfunktion. Dazu betrachten wir \(f''(x_0)=6(x_0-1)=0\). Wir formen um zu \(x_0-1=0\). Die Lösung der Gleichung lautet \(x_0=1\).
An der Stelle \({\color{green}{x_0=1}}\) lautet die dritte Ableitung \(f'''(x_0)=6\neq 0\). An der Stelle \({\color{green}{x_0=1}}\) hat die Funktion daher einen Wendepunkt.
Der Funktionsgraph der Funktion \(f\) sowie der Wendepunkt sind in der nächsten Grafik dargestellt.

Sattelpunkt bzw. Terrassenpunkt
Ein Sattelpunkt bzw. Terrassenpunkt ist ein Spezialfall unter den Wendepunkten: An der Stelle \(x_0\) einer dreimal differenzierbaren reellen Funktion \(f\) liegt ein Sattelpunkt vor, wenn \(f'(x_0) = 0\), \(f''(x_0) = 0\) und \(f'''(x_0) \neq 0\) sind. Die Sattelpunkte bzw. Terrassenpunkte einer dreimal differenzierbaren Funktion können durch folgende Schritte berechnet werden:- Berechnen der ersten Ableitungsfunktion \(f'\).
- Berechnen der zweiten Ableitungsfunktion \(f''\).
- Ermittlen der Nullstellen \(x_0\) der zweiten Ableitungsfunktion: \(f''(x_0)=0\).
- Einsetzen der Nullstellen in die erste Ableitungsfunktion: Nur jene \(x_0\) für die \(f'(x_0)=0\) gilt, werden weiter betrachtet.
- Berechnen der dritten Ableitungsfunktion \(f''\).
- Einsetzen der weiter betrachteten Nullstellen in die dritte Ableitungsfunktion:
- Ist \(f'''(x_0) \neq 0\), so ist ein Sattelpunkt bzw. Terrassenpunkt gegeben.
- Ist \(f'''(x_0)=0\), so sind weitere Untersuchungen notwendig (Es kann ein Sattelpunkt bzw. Terrassenpunkt gegeben sein).
Sei \(f(x)=3+(x-2)^3\). Die Ableitungsfunktion lautet \(f'(x)=3(x-2)^2\). Die zweite Ableitungsfunktion lautet \(f''(x)=6(x-2)\). Die dritte Ableitungsfunktion lautet \(f'''(x)=6\).
Wir suchen nun die Nullstellen der zweiten Ableitungsfunktion. Dazu betrachten wir \(f''(x_0)=6(x_0-2)=0\). Wir formen um zu \(x_0-2=0\). Die Lösung der Gleichung lautet \(x_0=2\).
Wir setzen nun in die erste Ableitungsfunktion ein: \(f'(2)=3(2-2)^2=0\). An der Stelle \(x_0=2\) ist also die Steigung gleich Null.
An der Stelle \({\color{green}{x_0=1}}\) lautet die erste Ableitung \(f'(x_0)=3(2-2)^2=0\) und die dritte Ableitung \(f'''(x_0)=6\neq 0\). An der Stelle \({\color{green}{x_0=2}}\) hat die Funktion daher einen Sattelpunkt bzw. Terrassenpunkt.
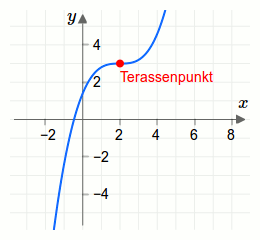
Der Funktionsgraph der Funktion \(f\) sowie der Sattelpunkt sind in der nächsten Grafik dargestellt.
Wir suchen nun die Nullstellen der zweiten Ableitungsfunktion. Dazu betrachten wir \(f''(x_0)=6(x_0-2)=0\). Wir formen um zu \(x_0-2=0\). Die Lösung der Gleichung lautet \(x_0=2\).
Wir setzen nun in die erste Ableitungsfunktion ein: \(f'(2)=3(2-2)^2=0\). An der Stelle \(x_0=2\) ist also die Steigung gleich Null.
An der Stelle \({\color{green}{x_0=1}}\) lautet die erste Ableitung \(f'(x_0)=3(2-2)^2=0\) und die dritte Ableitung \(f'''(x_0)=6\neq 0\). An der Stelle \({\color{green}{x_0=2}}\) hat die Funktion daher einen Sattelpunkt bzw. Terrassenpunkt.
Der Funktionsgraph der Funktion \(f\) sowie der Sattelpunkt sind in der nächsten Grafik dargestellt.
Zu den interaktiven Aufgaben → Wendepunkt Berechnen - Übungsaufgaben
Eventuell sind folgende Aufgaben interessant:
Zu den interaktiven Aufgaben → Wendepunkt Definition - Übungsaufgaben
Hat alles, was man braucht: Taschenrechner CASIO FX-991DE X *
Die mit Sternchen (*) gekennzeichneten Verweise sind sogenannte Provisions-Links. Für dich entstehen dabei keine Nachteile!