Wendepunkt Definition
Ein Wendepunkt ist ein Punkt auf einer Funktion, an dem sich das Vorzeichen der Krümmung der Funktion ändert.
Anschaulich bedeutet dies, dass der Funktionsgraph dort von einer Rechtskurve (konkave Kurve) zu einer Linkskurve (konvexe Kurve) wechselt oder umgekehrt.
Was ist der Unterschied zwischen einem Wendepunkt und einer Wendestelle?
Der Unterschied zwischen einem Wendepunkt und einer Wendestelle liegt im Unterschied zwischen den Begriffen Punkt und Stelle. Während \(x\) eine Stelle ist, ist \(\begin{pmatrix}x\\y\end{pmatrix}\) ein Punkt. Mit Stelle ist also nur der \(x\)-Wert gemeint. Mit Punkt ist das Wertepaar \((x|y)\) gemeint.Hat eine Funktion \(f\) einen Wendepunkt bei \((x|y)\), so hat sie eine Wendestelle bei \(x\). Anders herum kann man sagen: Hat eine Funktion \(f\) eine Wendestelle bei \(x\), so hat sie einen Wendepunkt bei \(x|f(x))=(x|y)\).
Der Unterschied liegt also darin, dass bei einem Wendepunkt der \(y\)-Wert mitangegeben ist und bei einer Wendestelle nicht.
Die Funktion \(f(x)=x+(x-1)^3\) hat an der Stelle \(x=1\) eine Wendestelle. Der Wendepunkt lautet \(\begin{pmatrix}1\\f(1)\end{pmatrix}=\begin{pmatrix}1\\1\end{pmatrix}\). Der Funktionsgraph der Funktion \(f\) sowie der Wendepunkt sind in der nächsten Grafik dargestellt.
Sattelpunkt bzw. Terassenpunkt
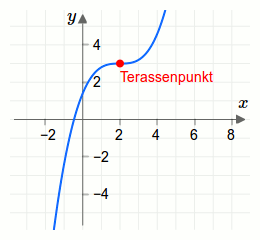
Es gibt einen besonderen Typ unter den Wendepunkten. Man nennt ihn Sattelpunkt bzw. Terassenpunkt. Ein Terassenpunkt ist ein Wendepunkt, an dessen Stelle die Funktion die Steigung Null hat.Die Funktion \(f(x)=3+(x-2)^3\) hat an der Stelle \(x=2\) einen Terassenpunkt. Der Terassenpunkt lautet \(\begin{pmatrix}2\\f(2)\end{pmatrix}=\begin{pmatrix}2\\3\end{pmatrix}\). Der Funktionsgraph der Funktion \(f\) sowie der Terassenpunkt sind in der nächsten Grafik dargestellt.
Hinweis: Man kann die Wendepunkte einer differenzierbaren Funktion mittels der Differentialrechnung ermitteln.
Zu den interaktiven Aufgaben → Wendepunkt Definition - Übungsaufgaben
Weiterführende Artikel:
Hat alles, was man braucht: Taschenrechner CASIO FX-991DE X *
Die mit Sternchen (*) gekennzeichneten Verweise sind sogenannte Provisions-Links. Für dich entstehen dabei keine Nachteile!