Kreuzprodukt bzw. äußeres Produkt

Ein Kreuzprodukt bzw. äußeres Produkt bzw. Vektorprodukt ist eine Multiplikation zweier Vektoren. Das Ergebnis ist ein Vektor der senkrecht auf beide Vektoren steht. Also ein Normalvektor zu beiden Vektoren. Man verwendet für das Multiplikationszeichen das Symbol \(\times\). Voraussetzung für die Durchführbarkeit ist, dass beide Vektoren jeweils genau drei Komponenten besitzen. Für Vektoren mit zwei Komponenten oder etwa mit vier Komponenten ist das Kreuzprodukt daher nicht definiert! Für Vektoren mit drei Komponenten ist das Kreuzprodukt durch folgenden Rechenschritt gegeben:

\[\begin{pmatrix}a_1\\a_2\\a_3\end{pmatrix}\times\begin{pmatrix}b_1\\b_2\\b_3\end{pmatrix}=\begin{pmatrix}a_2\cdot b_3-a_3\cdot b_2\\a_3\cdot b_1-a_1\cdot b_3\\a_1\cdot b_2-a_2\cdot b_1\end{pmatrix}\]

Es gibt auch einen interaktiven Online-Rechner zum Kreuzprodukt.

Beispiele und Aufgaben mit Lösungen

\[\begin{pmatrix}1\\0\\0\end{pmatrix}\times\begin{pmatrix}0\\1\\0\end{pmatrix}=\begin{pmatrix}0\cdot 0-0\cdot 1\\0\cdot 0-1\cdot 0\\1\cdot 1-0\cdot 0\end{pmatrix}=\begin{pmatrix}0\\0\\1\end{pmatrix}\]

\[\begin{pmatrix}0\\1\\0\end{pmatrix}\times\begin{pmatrix}1\\0\\0\end{pmatrix}=\begin{pmatrix}0\cdot 0-0\cdot 1\\0\cdot 0-1\cdot 0\\0\cdot 0-1\cdot 1\end{pmatrix}=\begin{pmatrix}0\\0\\-1\end{pmatrix}\]

\[\begin{pmatrix}1\\2\\3\end{pmatrix}\times\begin{pmatrix}4\\5\\6\end{pmatrix}=\begin{pmatrix}2\cdot 6-3\cdot 5\\3\cdot 4-1\cdot 6\\1\cdot 5-2\cdot 4\end{pmatrix}=\begin{pmatrix}-3\\6\\-3\end{pmatrix}\]

Zu den interaktiven Aufgaben → Kreuzprodukt - Übungsaufgaben

Flächeninhalt eines Parallelogramms

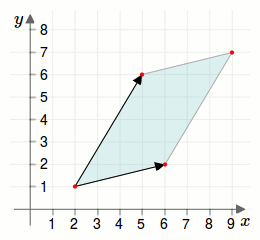
Man kann mit dem Kreuzprodukt den Flächeninhalt eines Parallelogramms berechnen, das zwei Vektoren aufspannen.

Wie groß ist die Fläche des Parallelogramms, dass durch die drei Punkte \(A=\begin{pmatrix}2\\1\end{pmatrix}\), \(B=\begin{pmatrix}6\\2\end{pmatrix}\) und \(C=\begin{pmatrix}5\\6\end{pmatrix}\) aufgespannt wird (siehe Grafik unterhalb)?

Wir erstellen die beiden Vektoren \(\overrightarrow{AB}=\vec{B}-\vec{A}=\begin{pmatrix}4\\1\end{pmatrix}\) und \(\overrightarrow{AC}=\vec{C}-\vec{A}=\begin{pmatrix}3\\5\end{pmatrix}\).
Um Vektoren mit drei Komponenten zu erhalten, fügen wir noch eine weitere Komponente hinzu. \(\vec{u}=\begin{pmatrix}4\\1\\0\end{pmatrix}\) sowie \(\vec{v}=\begin{pmatrix}3\\5\\0\end{pmatrix}\).
Der Flächeninhalt des Parallelogramms kann nun durch \(|\vec{u}\times\vec{v}|\) berechnet werden. \[\vec{u}\times\vec{v}=\begin{pmatrix}4\\1\\0\end{pmatrix}\times\begin{pmatrix}3\\5\\0\end{pmatrix}=\begin{pmatrix}0\\0\\17\end{pmatrix}\] Damit lautet der Flächeninhalt \(|\vec{u}\times\vec{v}|=17\).

Darstellung Flächeninhalt eines Parallelogramms

Normalvektor einer Ebene

Eine Ebene kann durch zwei (nicht parallelen) Vektoren und einem Punkt eindeutig festgelegt werden. Man kann das Kreuzprodukt verwenden, um einen Normalvektor einer Ebene zu berechnen.

Wie lautet ein Normalvektor der Ebene, die durch die Ebenengleichung \(\begin{pmatrix}x\\y\\z\end{pmatrix}=\begin{pmatrix}1\\3\\2\end{pmatrix}+s\cdot\begin{pmatrix}1\\1\\0\end{pmatrix}+t\cdot\begin{pmatrix}2\\0\\3\end{pmatrix}\) festgelgt ist?

Ein Normalvektor ist durch das Kreuzprodukt \[\begin{pmatrix}1\\1\\0\end{pmatrix}\times\begin{pmatrix}2\\0\\3\end{pmatrix}=\begin{pmatrix}3\\-3\\-2\end{pmatrix}\] gegeben.