Normalvektor
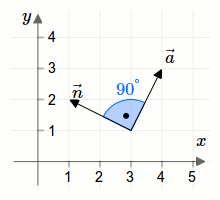
Ein Vektor ist ein Normalvektor bzw. Normalenvektor bezüglich eines anderen Vektors, wenn die jeweiligen Richtungen der Vektoren zueinander um \(90^{\circ}\) gedreht sind. Das Skalarprodukt eines Vektors und eines dazugehörigen Normalvektors ist gleich Null.In der folgenden Grafik ist ein Vektor \(\vec{a}=\begin{pmatrix}1\\2\end{pmatrix}\) und ein dazugehöriger Normalvektor \(\vec{n}=\begin{pmatrix}-2\\1\end{pmatrix}\) eingezeichnet.
Das Skalarprodukt der beiden Vektoren lautet \[\vec{a} \cdot \vec{n} =\begin{pmatrix}1\\2\end{pmatrix}\cdot \begin{pmatrix}-2\\1\end{pmatrix}=1\cdot (-2)+2\cdot 1=0\]
Das Skalarprodukt der beiden Vektoren lautet \[\vec{a} \cdot \vec{n} =\begin{pmatrix}1\\2\end{pmatrix}\cdot \begin{pmatrix}-2\\1\end{pmatrix}=1\cdot (-2)+2\cdot 1=0\]
Es ist \(\begin{pmatrix}3\\7\end{pmatrix}\cdot \begin{pmatrix}-7\\3\end{pmatrix}=0\). Damit ist \(\begin{pmatrix}3\\7\end{pmatrix}\) ein Normalvektor von \(\begin{pmatrix}-7\\3\end{pmatrix}\).
Es ist \(\begin{pmatrix}3\\7\end{pmatrix}\cdot \begin{pmatrix}-7\\3\end{pmatrix}=0\). Damit ist \(\begin{pmatrix}-7\\3\end{pmatrix}\) ein Normalvektor von \(\begin{pmatrix}3\\7\end{pmatrix}\).
Es ist \(\begin{pmatrix}1\\1\\-1\end{pmatrix}\cdot \begin{pmatrix}1\\0\\1\end{pmatrix}=0\). Damit ist \(\begin{pmatrix}1\\1\\-1\end{pmatrix}\) ein Normalvektor von \(\begin{pmatrix}1\\0\\1\end{pmatrix}\) und umgekehrt.
Es ist \(\begin{pmatrix}1\\0\\0\\0\end{pmatrix}\cdot \begin{pmatrix}0\\1\\0\\0\end{pmatrix}=0\) und es ist \(\begin{pmatrix}1\\0\\0\\0\end{pmatrix}\cdot \begin{pmatrix}0\\0\\1\\0\end{pmatrix}=0\). Damit sind \(\begin{pmatrix}0\\1\\0\\0\end{pmatrix}\) und \(\begin{pmatrix}0\\0\\1\\0\end{pmatrix}\) Normalvektoren des Vektors \(\begin{pmatrix}1\\0\\0\\0\end{pmatrix}\).
Zu den interaktiven Aufgaben → Normalvektor - Übungsaufgaben
Weiterführende Artikel:
Hat alles, was man braucht: Taschenrechner CASIO FX-991DE X *
Die mit Sternchen (*) gekennzeichneten Verweise sind sogenannte Provisions-Links. Für dich entstehen dabei keine Nachteile!