Krümmung berechnen
Die Krümmung einer zweifach differenzierbaren Funktion kann durch die zweifache Ableitung berechnet werden. Man unterscheidet zwischen keiner Krümmung, Linkskrümmung und Rechtskrümmung.Eine Funktion ist an einer Stelle \(x_0\) nicht gekrümmt, wenn dort \(f''(x_0)=0\) ist.
Eine Linkskrümmung einer Funktion \(f\) an der Stelle \(x_0\) liegt vor, wenn \(f''(x_0) > 0\) ist. Man sagt auch, dass die Funktion dort linksgekrümmt, positiv gekrümmt oder konvex ist.
Eine Rechtskrümmung einer Funktion \(f\) an der Stelle \(x_0\) liegt vor, wenn \(f''(x_0) < 0\) ist. Man sagt auch, dass die Funktion dort rechtsgekrümmt, negativ gekrümmt oder konkav ist.
Aufgaben mit Lösungen
Es ist die Funktion \({\color{blue}{f(x)=x^2}}\) gegeben. Wie lautet die Krümmung dieser Funktion?
Die Ableitungsfunktion lautet \(f'(x)=2x\).
Die Ableitungsfunktion der Ableitungsfunktion (=zweite Ableitungsfunktion) lautet \(f''(x)=2 > 0\).
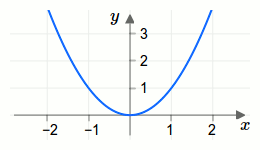
Die zweite Ableitung ist überall positiv. Damit liegt bei der Funktion überall eine Linkskrümmung vor. Daher ist die gesamte Funktion konvex.
Der Funktionsgraph der Funktion \(f\) ist in der nächsten Grafik dargestellt.
Die Ableitungsfunktion der Ableitungsfunktion (=zweite Ableitungsfunktion) lautet \(f''(x)=2 > 0\).
Die zweite Ableitung ist überall positiv. Damit liegt bei der Funktion überall eine Linkskrümmung vor. Daher ist die gesamte Funktion konvex.
Der Funktionsgraph der Funktion \(f\) ist in der nächsten Grafik dargestellt.
Es ist die Funktion \({\color{red}{f(x)=-x^2}}\) gegeben. Wie lautet die Krümmung dieser Funktion?
Die Ableitungsfunktion lautet \(f'(x)=-2x\).
Die zweite Ableitungsfunktion lautet \(f''(x)=-2 < 0\).
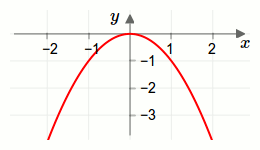
Die zweite Ableitung ist überall negativ. Damit liegt bei der Funktion überall eine Rechtskrümmung vor. Daher ist die gesamte Funktion konkav.
Der Funktionsgraph der Funktion \(f\) ist in der nächsten Grafik dargestellt.
Die zweite Ableitungsfunktion lautet \(f''(x)=-2 < 0\).
Die zweite Ableitung ist überall negativ. Damit liegt bei der Funktion überall eine Rechtskrümmung vor. Daher ist die gesamte Funktion konkav.
Der Funktionsgraph der Funktion \(f\) ist in der nächsten Grafik dargestellt.
Es ist die Funktion \(f(x)=x^2+\frac{1}{3}\cdot x^3\) gegeben. Untersuche das Krümmungsverhalten der Funktion!
Die Ableitungsfunktion lautet \(f'(x)=2x+x^2\).
Die zweite Ableitungsfunktion lautet \(f''(x)=2+2x\).
Für \(2+2x > 0\) liegt eine Linkskrümmung vor. Das ist bei \({\color{blue}{x > -1}}\).
Für \(2+2x < 0\) liegt eine Rechtskrümmung vor. Das ist bei \({\color{red}{x < -1}}\).
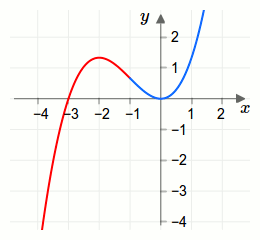
Der Funktionsgraph der Funktion \(f\) ist in der nächsten Grafik dargestellt. Der rechtsgekrümmte/konkave Teil der Funktion ist rot und der linksgekrümmte/konvexe Teil der Funktion ist blau dargestellt.
Die zweite Ableitungsfunktion lautet \(f''(x)=2+2x\).
Für \(2+2x > 0\) liegt eine Linkskrümmung vor. Das ist bei \({\color{blue}{x > -1}}\).
Für \(2+2x < 0\) liegt eine Rechtskrümmung vor. Das ist bei \({\color{red}{x < -1}}\).
Der Funktionsgraph der Funktion \(f\) ist in der nächsten Grafik dargestellt. Der rechtsgekrümmte/konkave Teil der Funktion ist rot und der linksgekrümmte/konvexe Teil der Funktion ist blau dargestellt.
Zu den interaktiven Aufgaben → Krümmung einer Funktion - Übungsaufgaben
Weiterführende Artikel:
Hat alles, was man braucht: Taschenrechner CASIO FX-991DE X *
Die mit Sternchen (*) gekennzeichneten Verweise sind sogenannte Provisions-Links. Für dich entstehen dabei keine Nachteile!