Schnittpunkt zweier Funktionen

Ein Schnittpunkt zweier Funktionen ist ein Punkt, der ein Wertepaar beider Funktionen ist. Anders formuliert liegt der Punkt gleichzeitig auf beiden Funktionen.

Ist \(x_s\) der x-Wert des Schnittpunktes der beiden Funktionen \(f\) und \(g\), so gilt \[f(x_s)=g(x_s)\]

Aufgaben mit Lösungen

Wie lautet der Schnittpunkt der Funktionen \(f(x)=1+2x\) und \(g(x)=2+x\) ?

Es gilt \[\begin{array}{ccc} f(x_s)&=&g(x_s) \\ 1+2x_s&=&2+x_s \\ 2x_s-x_s&=&2-1 \\ x_s&=&1 \end{array}\]Der y-Wert ist durch \(y_s=f(x_s)=3\) oder durch \(y_s=g(x_s)=3\) gegeben.
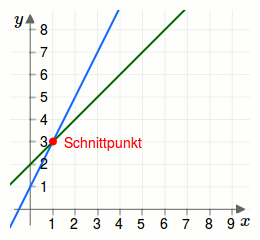
Der Schnittpunkt lautet somit \(\begin{pmatrix}1\\3\end{pmatrix}\). Siehe folgende Grafik.

Wie lauten die Schnittpunkte der Funktionen \(f(x)=x^2\) und \(g(x)=x+2\) ?

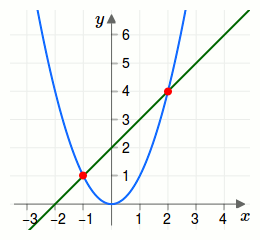
Für den Schnittpunkt \((x_s|y_s)\) gilt \(f(x_s)=g(x_s)\). Wir setzen ein und rechnen aus. \[f(x_s)=g(x_s)\] \[x_s^2=x_s+2\qquad\color{gray}{|-x_s-2}\] \[x_s^2-x_s-2=0\] Mit der PQ-Formel für quadratische Gleichungen erhält man die Lösungen \(x=2\) oder \(x=-1\). Es ist \(f(2)=2^2=4\). Es ist \(f(-1)=1\). Damit gibt es zwei Schnittpunkte: \(\begin{pmatrix}2\\4\end{pmatrix}\) und \(\begin{pmatrix}-1\\1\end{pmatrix}\). Diese sind in der nächsten Grafik eingezeichnet.

Zu den interaktiven Aufgaben → Schnittpunkt zweier Funktionen - Übungsaufgaben