Mittlere / durchschnittliche Geschwindigkeit

In diesem Artikel wird der Begriff 'mittlere / durchschnittliche Geschwindigkeit' erklärt und eine Formel angegeben.

Da es vorkommt, dass sich die Geschwindigkeit im zeitlichen Verlauf verändert, ist man oft an einer mittleren Geschwindigkeit interessiert.

Die mittlere Geschwindigkeit ist die gesamte zurückgelegte Distanz \(\Delta x\) geteilt durch die dabei insgesamt verstrichene Zeit \(\Delta t\) \[v=\frac{\Delta x}{\Delta t}\]

Bewegt sich ein Objekt in der folgenden Grafik von der Position A entlang der Geraden zur Position B und verstreicht dabei die Zeit \(\Delta t\), so ist die durchschnittliche Geschwindigkeit mit der sich das Objekt bewegt hat, durch die Distanz \(\Delta x\) geteilt durch \(\Delta t\) gegeben.

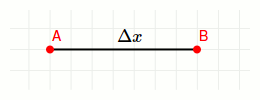
Die Länge \(\Delta x\) stellt den Ortsunterschied zwischen den Punkten \(A\) und \(B\) dar.

Ein Auto fährt 30 Minuten mit einer konstanten Geschwindigkeit von 120 km/h. Danach fährt es eine Stunde mit einer konstanten Geschwindigkeit von 80 km/h. Wie lautet die mittlere Geschwindigkeit der gesamten zurückgelegten Strecke?

Die zurückgelegte Distanz nach 30 Minuten kann berechnet werden durch \[v_1=\frac{\Delta x_1}{\Delta t_1}\] \[120\text{ km/h}=\frac{\Delta x_1}{0{,}5\text{ h}}\] \[\Delta x_1=60\text{ km}\] Die zurückgelegte zweite Distanz kann berechnet werden durch \[v_2=\frac{\Delta x_2}{\Delta t_2}\] \[80\text{ km/h}=\frac{\Delta x_2}{1\text{ h}}\] \[\Delta x_2=80\text{ km}\] Die gesamte zurückgelegte Distanz lautet \(\Delta x=\Delta x_1+\Delta x_2=60\text{ km}+80\text{ km}=140\text{ km}\).
Die gesamte Zeitdauer ist \[\Delta t=\Delta t_1+\Delta t_2=0{,}5\text{ h}+1\text{ h}=1{,}5\text{ h}\]

Die mittlere Geschwindigkeit der gesamten zurückgelegten Strecke ist gegeben durch \[v=\frac{\Delta x}{\Delta t}=\frac{140\text{ km}}{1{,}5\text{ h}}=93{,}3\text{ km/h}\]

Weiterführende Artikel: