Normalverteilung und Standardnormalverteilung
Die Normalverteilung bzw. Gauß-Verteilung ist eine stetige Wahrscheinlichkeitsverteilung. Die Normalverteilung ist durch die Wahrscheinlichkeitsdichtefunktion\[f(x)=\frac{1}{\sigma \sqrt{2\pi}}e^{-\frac{1}{2\sigma ^2}(x-\mu)^2}\] definiert. Dabei ist \(\mu\) der Erwartungswert und \(\sigma\) die Standardabweichung der Verteilung. In der folgenden Grafik ist der Funktionsgraph der Wahrscheinlichkeitsdichtefunktion \(f(x)=\frac{1}{\sqrt{2\pi}}e^{-\frac{1}{2}(x-3)^2}\) dargestellt: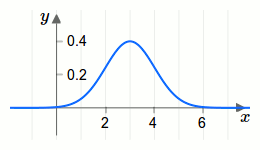 Bei einer stetigen Wahrscheinlichkeitsverteilung ist es nicht sinnvoll zu fragen, wie wahrscheinlich es ist, dass die Zufallsvariable \(X\) einen bestimmten Wert annimmt. Die Antwort wäre dann immer Null! Ist doch klar, denn es gibt unendlich viele andere Werte, die die Zufallsvariable annehmen könnte.
Bei einer stetigen Wahrscheinlichkeitsverteilung ist es nicht sinnvoll zu fragen, wie wahrscheinlich es ist, dass die Zufallsvariable \(X\) einen bestimmten Wert annimmt. Die Antwort wäre dann immer Null! Ist doch klar, denn es gibt unendlich viele andere Werte, die die Zufallsvariable annehmen könnte.Es ist weitaus sinnvoller zu fragen, wie wahrscheinlich es ist, dass die Zufallsvariable \(X\) irgend einen Wert innerhalb eines bestimmten Intervalls \([a,b]\) annimmt. In der folgenden Grafik ist das Intervall mit \(a=2\) und \(b=3{,}5\) eingezeichnet:
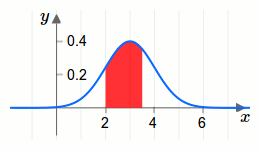 Die Wahrscheinlichkeit, dass die Zufallsvariable \(X\) einen Wert innerhalb des Intervalls annimmt, ist gleich der markierten Fläche (dividiert durch die gesamte Fläche zwischen der Funktion und der x-Achse, welche jedoch Eins ist – deswegen übrigens der Faktor \(\frac{1}{\sigma \sqrt{2\pi}}\)).
Die Wahrscheinlichkeit, dass die Zufallsvariable \(X\) einen Wert innerhalb des Intervalls annimmt, ist gleich der markierten Fläche (dividiert durch die gesamte Fläche zwischen der Funktion und der x-Achse, welche jedoch Eins ist – deswegen übrigens der Faktor \(\frac{1}{\sigma \sqrt{2\pi}}\)).Um die Fläche und damit die Wahrscheinlichkeit zu berechnen, müssen wir folgendes Integral lösen\[P(a\leq X\leq b)=\int _a ^b f(x)dx=\int _a ^b \frac{1}{\sigma \sqrt{2\pi}}e^{-\frac{1}{2\sigma ^2}(x-\mu)^2}dx\]Da dieses Integral nicht exakt lösbar ist, verwendet man Tabellen zum Nachschlagen der Lösungen. Um die Tabellen nutzen zu können, muss man üblicherweise die Variable \(z=\frac{x-\mu}{\sigma}\) ersetzen. Wir haben nun das Integral\[P(z_1\leq Z\leq z_2)=\int _{z_1} ^{z_2} \frac{1}{\sqrt{2\pi}}e^{-\frac{1}{2}z^2}dz\]wobei \(z_1=\frac{a-\mu}{\sigma}\) und \(z_2=\frac{b-\mu}{\sigma}\).
Die Funktion \[f(x)=\frac{1}{\sqrt{2\pi}}e^{-\frac{1}{2}x^2}\] ist die Wahrscheinlichkeitsdichtefunktion der sogenannten Standardnormalverteilung. Das ist die Normalverteilung mit \(\mu=0\) und \(\sigma=1\).
Integraltabelle zur Standardnormalverteilung
In jeder Formelsammlung sollte auch eine Tabelle zum Nachschlagen der Flächeninhalte des Integrals \[\Phi(z)=\int _{-\infty} ^{z} \frac{1}{\sqrt{2\pi}}e^{-\frac{1}{2}x^2}dx\]vorhanden sein. Die Tabelle könnte wie folgt aussehen:| \(z\) | \(\Phi (z)\) | \(\Phi (z+0{,}01)\) | \(\Phi (z+0{,}02)\) | \(\Phi (z+0{,}03)\) | \(\Phi (z+0{,}04)\) | \(\Phi (z+0{,}05)\) | \(\Phi (z+0{,}06)\) | \(\Phi (z+0{,}07)\) | \(\Phi (z+0{,}08)\) | \(\Phi (z+0{,}09)\) |
| 0,0 | 0,50000 | 0,50399 | 0,50798 | 0,51197 | 0,51595 | 0,51994 | 0,52392 | 0,52790 | 0,53188 | 0,53586 |
| 0,1 | 0,53983 | 0,54380 | 0,54776 | 0,55172 | 0,55567 | 0,55962 | 0,56356 | 0,56749 | 0,57142 | 0,57535 |
| 0,2 | 0,57926 | 0,58317 | 0,58706 | 0,59095 | 0,59483 | 0,59871 | 0,60257 | 0,60642 | 0,61026 | 0,61409 |
| 0,3 | 0,61791 | 0,62172 | 0,62552 | 0,62930 | 0,63307 | 0,63683 | 0,64058 | 0,64431 | 0,64803 | 0,65173 |
| 0,4 | 0,65542 | 0,65910 | 0,66276 | 0,66640 | 0,67003 | 0,67364 | 0,67724 | 0,68082 | 0,68439 | 0,68793 |
| 0,5 | 0,69146 | 0,69497 | 0,69847 | 0,70194 | 0,70540 | 0,70884 | 0,71226 | 0,71566 | 0,71904 | 0,72240 |
| 0,6 | 0,72575 | 0,72907 | 0,73237 | 0,73565 | 0,73891 | 0,74215 | 0,74537 | 0,74857 | 0,75175 | 0,75490 |
| 0,7 | 0,75804 | 0,76115 | 0,76424 | 0,76730 | 0,77035 | 0,77337 | 0,77637 | 0,77935 | 0,78230 | 0,78524 |
| 0,8 | 0,78814 | 0,79103 | 0,79389 | 0,79673 | 0,79955 | 0,80234 | 0,80511 | 0,80785 | 0,81057 | 0,81327 |
| 0,9 | 0,81594 | 0,81859 | 0,82121 | 0,82381 | 0,82639 | 0,82894 | 0,83147 | 0,83398 | 0,83646 | 0,83891 |
| 1,0 | 0,84134 | 0,84375 | 0,84614 | 0,84849 | 0,85083 | 0,85314 | 0,85543 | 0,85769 | 0,85993 | 0,86214 |
| 1,1 | 0,86433 | 0,86650 | 0,86864 | 0,87076 | 0,87286 | 0,87493 | 0,87698 | 0,87900 | 0,88100 | 0,88298 |
| 1,2 | 0,88493 | 0,88686 | 0,88877 | 0,89065 | 0,89251 | 0,89435 | 0,89617 | 0,89796 | 0,89973 | 0,90147 |
| 1,3 | 0,90320 | 0,90490 | 0,90658 | 0,90824 | 0,90988 | 0,91149 | 0,91309 | 0,91466 | 0,91621 | 0,91774 |
| 1,4 | 0,91924 | 0,92073 | 0,92220 | 0,92364 | 0,92507 | 0,92647 | 0,92785 | 0,92922 | 0,93056 | 0,93189 |
| 1,5 | 0,93319 | 0,93448 | 0,93574 | 0,93699 | 0,93822 | 0,93943 | 0,94062 | 0,94179 | 0,94295 | 0,94408 |
| 1,6 | 0,94520 | 0,94630 | 0,94738 | 0,94845 | 0,94950 | 0,95053 | 0,95154 | 0,95254 | 0,95352 | 0,95449 |
| 1,7 | 0,95543 | 0,95637 | 0,95728 | 0,95818 | 0,95907 | 0,95994 | 0,96080 | 0,96164 | 0,96246 | 0,96327 |
| 1,8 | 0,96407 | 0,96485 | 0,96562 | 0,96638 | 0,96712 | 0,96784 | 0,96856 | 0,96926 | 0,96995 | 0,97062 |
| 1,9 | 0,97128 | 0,97193 | 0,97257 | 0,97320 | 0,97381 | 0,97441 | 0,97500 | 0,97558 | 0,97615 | 0,97670 |
| 2,0 | 0,97725 | 0,97778 | 0,97831 | 0,97882 | 0,97932 | 0,97982 | 0,98030 | 0,98077 | 0,98124 | 0,98169 |
| 2,1 | 0,98214 | 0,98257 | 0,98300 | 0,98341 | 0,98382 | 0,98422 | 0,98461 | 0,98500 | 0,98537 | 0,98574 |
| 2,2 | 0,98610 | 0,98645 | 0,98679 | 0,98713 | 0,98745 | 0,98778 | 0,98809 | 0,98840 | 0,98870 | 0,98899 |
| 2,3 | 0,98928 | 0,98956 | 0,98983 | 0,99010 | 0,99036 | 0,99061 | 0,99086 | 0,99111 | 0,99134 | 0,99158 |
| 2,4 | 0,99180 | 0,99202 | 0,99224 | 0,99245 | 0,99266 | 0,99286 | 0,99305 | 0,99324 | 0,99343 | 0,99361 |
| 2,5 | 0,99379 | 0,99396 | 0,99413 | 0,99430 | 0,99446 | 0,99461 | 0,99477 | 0,99492 | 0,99506 | 0,99520 |
| 2,6 | 0,99534 | 0,99547 | 0,99560 | 0,99573 | 0,99585 | 0,99598 | 0,99609 | 0,99621 | 0,99632 | 0,99643 |
| 2,7 | 0,99653 | 0,99664 | 0,99674 | 0,99683 | 0,99693 | 0,99702 | 0,99711 | 0,99720 | 0,99728 | 0,99736 |
| 2,8 | 0,99744 | 0,99752 | 0,99760 | 0,99767 | 0,99774 | 0,99781 | 0,99788 | 0,99795 | 0,99801 | 0,99807 |
| 2,9 | 0,99813 | 0,99819 | 0,99825 | 0,99831 | 0,99836 | 0,99841 | 0,99846 | 0,99851 | 0,99856 | 0,99861 |
| 3,0 | 0,99865 | 0,99869 | 0,99874 | 0,99878 | 0,99882 | 0,99886 | 0,99889 | 0,99893 | 0,99896 | 0,99900 |
| 3,1 | 0,99903 | 0,99906 | 0,99910 | 0,99913 | 0,99916 | 0,99918 | 0,99921 | 0,99924 | 0,99926 | 0,99929 |
| 3,2 | 0,99931 | 0,99934 | 0,99936 | 0,99938 | 0,99940 | 0,99942 | 0,99944 | 0,99946 | 0,99948 | 0,99950 |
| 3,3 | 0,99952 | 0,99953 | 0,99955 | 0,99957 | 0,99958 | 0,99960 | 0,99961 | 0,99962 | 0,99964 | 0,99965 |
| 3,4 | 0,99966 | 0,99968 | 0,99969 | 0,99970 | 0,99971 | 0,99972 | 0,99973 | 0,99974 | 0,99975 | 0,99976 |
| 3,5 | 0,99977 | 0,99978 | 0,99978 | 0,99979 | 0,99980 | 0,99981 | 0,99981 | 0,99982 | 0,99983 | 0,99983 |
| 3,6 | 0,99984 | 0,99985 | 0,99985 | 0,99986 | 0,99986 | 0,99987 | 0,99987 | 0,99988 | 0,99988 | 0,99989 |
| 3,7 | 0,99989 | 0,99990 | 0,99990 | 0,99990 | 0,99991 | 0,99991 | 0,99992 | 0,99992 | 0,99992 | 0,99992 |
| 3,8 | 0,99993 | 0,99993 | 0,99993 | 0,99994 | 0,99994 | 0,99994 | 0,99994 | 0,99995 | 0,99995 | 0,99995 |
| 3,9 | 0,99995 | 0,99995 | 0,99996 | 0,99996 | 0,99996 | 0,99996 | 0,99996 | 0,99996 | 0,99997 | 0,99997 |
| 4,0 | 0,99997 | 0,99997 | 0,99997 | 0,99997 | 0,99997 | 0,99997 | 0,99998 | 0,99998 | 0,99998 | 0,99998 |
Beispiele
Um das Integral \(\Phi(3)=\int _{-\infty} ^{3} \frac{1}{\sqrt{2\pi}}e^{-\frac{1}{2}x^2}dx\) zu Lösen, sieht man bei der Tabelle nach, welcher Wert bei \(z=3\) steht. Damit ist \(\Phi(3)=0{,}99865\).
Um das Integral \(\Phi(1{,}47)=\int _{-\infty} ^{1{,}47} \frac{1}{\sqrt{2\pi}}e^{-\frac{1}{2}x^2}dx\) zu Lösen, sieht man bei der Tabelle nach, welcher Wert bei \(z=1{,}47\) steht. Damit ist \(\Phi(1{,}47)=0{,}92922\).
Was macht man, wenn \(z\) negativ ist? Dann kann man die Gleichung \[\Phi (-z)=1-\Phi (z)\] verwenden.
Um das Integral \(\Phi(-1)=\int _{-\infty} ^{-1} \frac{1}{\sqrt{2\pi}}e^{-\frac{1}{2}x^2}dx\) zu Lösen, schreiben wir \[\Phi (-1)=1-\Phi (1)\] und sehen bei der Tabelle nach, welcher Wert bei \(z=1\) steht. Es ist \(\Phi(1)=0{,}84134\). Damit ist \(\Phi (-1)=1-\Phi (1)=1-0{,}84134=0{,}15866\)
Um das Integral \(I=\int _{-1} ^{1{,}3} \frac{1}{\sqrt{2\pi}}e^{-\frac{1}{2}x^2}dx\) zu Lösen, schreiben wird das Integral wie folgt an:\[\int _{-1} ^{1{,}3} \ldots dx=\int _{-\infty} ^{1{,}3} \ldots dx-\int _{-\infty} ^{-1} \ldots dx\]Also haben wir \(I=\Phi (1{,}3)-\Phi (-1)=\Phi (1{,}3) - 1 +\Phi (1)=0{,}90320-1+0{,}84134=0{,}74454\).
Zu den interaktiven Aufgaben → Normalverteilung - Übungsaufgaben
Weiterführende Artikel:
Hat alles, was man braucht: Taschenrechner CASIO FX-991DE X *
Die mit Sternchen (*) gekennzeichneten Verweise sind sogenannte Provisions-Links. Für dich entstehen dabei keine Nachteile!