Vektoren addieren
Die Addition zweier Vektoren ist durch komponentenweises Addieren gegeben. Das Ergebnis ist wiederum ein Vektor. Man darf dabei nur Vektoren miteinander addieren, die gleich viele Komponenten haben.Die Vektoraddition der beiden Vektoren \(\vec{A}=\begin{pmatrix}a\\c\end{pmatrix}\) und \(\vec{B}=\begin{pmatrix}b\\d\end{pmatrix}\) ist durch
\[\vec{A}+\vec{B}=\begin{pmatrix}a\\c\end{pmatrix}+\begin{pmatrix}b\\d\end{pmatrix}=\begin{pmatrix}a+b\\c+d\end{pmatrix}\]
gegeben.
Wir sehen uns ein paar Beispiele an.
Beispiele und Aufgaben mit Lösungen
Es sind die beiden Vektoren \(\vec{A}=\begin{pmatrix}1\\5\end{pmatrix}\) und \(\vec{B}=\begin{pmatrix}4\\2\end{pmatrix}\) gegeben. Wie lautet die Summe dieser beiden Vektoren?
\[\vec{A}+\vec{B}=\begin{pmatrix}1\\5\end{pmatrix}+\begin{pmatrix}4\\2\end{pmatrix}=\begin{pmatrix}1+4\\5+2\end{pmatrix}=\begin{pmatrix}5\\7\end{pmatrix}\]
Es sind die beiden Vektoren \(\vec{A}=\begin{pmatrix}1\\2\\3\end{pmatrix}\) und \(\vec{B}=\begin{pmatrix}-1\\-1\\1\end{pmatrix}\) gegeben. Wie lautet die Summe der beiden Vektoren?
\[\vec{A}+\vec{B}=\begin{pmatrix}1\\2\\3\end{pmatrix}+\begin{pmatrix}-1\\-1\\1\end{pmatrix}=\begin{pmatrix}1+(-1)\\2+(-1)\\3+1\end{pmatrix}=\begin{pmatrix}0\\1\\4\end{pmatrix}\]
Die Vektoren \(\vec{A}=\begin{pmatrix}1\\5\end{pmatrix}\) und \(\vec{B}=\begin{pmatrix}-1\\-1\\1\end{pmatrix}\) können nicht addiert werden, da sie unterschiedlich viele Komponenten besitzen!
Addition von Vektoren durch Parallelverschiebung
Die geometrische Darstellung einer Addition zweier Vektoren wird durch eine Parallelverschiebung erreicht. Betrachten wir dazu die beiden Vektoren aus der ersten Aufgabe als Pfeile:
Zu den interaktiven Aufgaben → Addition von Vektoren - Übungsaufgaben
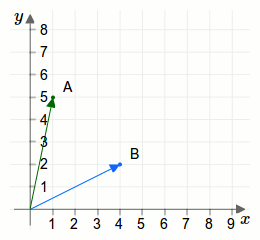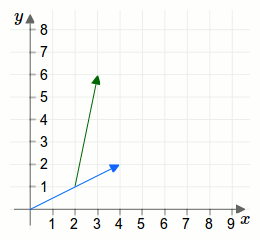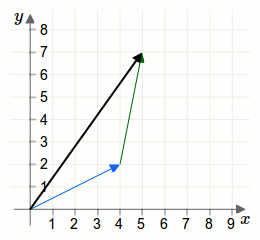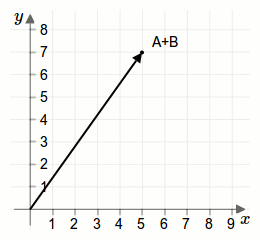
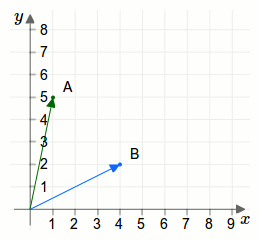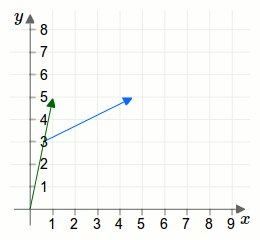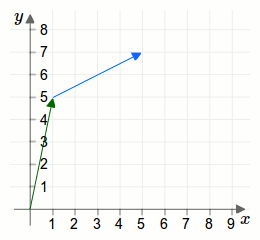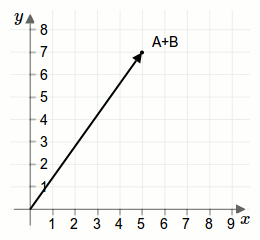
Weiterführende Artikel:
Hat alles, was man braucht: Taschenrechner CASIO FX-991DE X *
Die mit Sternchen (*) gekennzeichneten Verweise sind sogenannte Provisions-Links. Für dich entstehen dabei keine Nachteile!