Skalarmultiplikation
Die Skalarmultiplikation ist die Multiplikation eines Vektors mit einem Skalar (eine reelle oder komplexe Zahl). Dabei wird jede Komponente des Vektors mit dem Skalar multipliziert. Damit ist das Ergebnis ein Vektor. Ist ein Skalar positiv, dann bleibt die Richtung des Vektors erhalten, ist ein Skalar negativ, dann zeigt der resultierende Vektor in die entgegengesetzte Richtung.Beispiele
Wir haben den Vektor
\[\vec{Q}=\begin{pmatrix}2\\1\end{pmatrix}\]
gegeben und multiplizieren diesen mit einer Zahl:
\[\vec{R}=3\cdot \vec{Q}=3\cdot \begin{pmatrix}2\\1\end{pmatrix}=\begin{pmatrix}3 \cdot 2\\3 \cdot 1\end{pmatrix}=\begin{pmatrix}6\\3\end{pmatrix}\]
Macht diese Multiplikation Sinn? Wir können die Multiplikation in diesem Fall (da wir den Vektor \(\vec{Q}\) mit einer ganzen Zahl multiplizieren) auch als Vektoraddition umschreiben!
\[\vec{R}=3\cdot \vec{Q} =\vec{Q}+\vec{Q}+\vec{Q}=\begin{pmatrix}2\\1\end{pmatrix}+\begin{pmatrix}2\\1\end{pmatrix}+\begin{pmatrix}2\\1\end{pmatrix}=\begin{pmatrix}2+2+2\\1+1+1\end{pmatrix}=\begin{pmatrix}6\\3\end{pmatrix}\]
Überlegen wir uns dies geometrisch. In der folgenden Animation sind die Vektoren \(\vec{Q}\) und \(\vec{R}\) als Pfeile/Zeiger eingezeichnet:
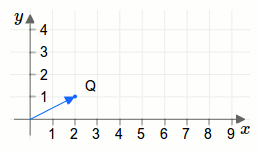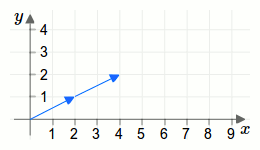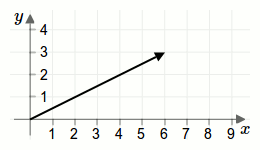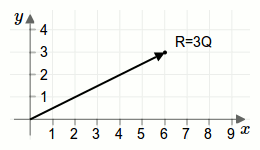Wenn man den Pfeil/Zeiger der nach \(\vec{Q}\) zeigt, noch weitere zweimal aufzeichnet, also dreimal so lange als ursprünglich, dann ergeben die insgesamt drei Pfeile genau den Pfeil, der nach \(\vec{R}\) zeigt.
Das funktioniert nicht nur mit ganzen Zahlen, sondern auch mit reellen Zahlen oder auch mit komplexen Zahlen!
Wenn man den Pfeil/Zeiger der nach \(\vec{Q}\) zeigt, noch weitere zweimal aufzeichnet, also dreimal so lange als ursprünglich, dann ergeben die insgesamt drei Pfeile genau den Pfeil, der nach \(\vec{R}\) zeigt.Das funktioniert nicht nur mit ganzen Zahlen, sondern auch mit reellen Zahlen oder auch mit komplexen Zahlen!
Die Skalarmultiplikation\[\color{blue}{2{,}5}\cdot \begin{pmatrix}2\\1\\-1\end{pmatrix}=\begin{pmatrix}\color{blue}{2{,}5}\cdot 2\\\color{blue}{2{,}5}\cdot 1\\\color{blue}{2{,}5}\cdot (-1)\end{pmatrix}=\begin{pmatrix}5\\2{,}5\\-2{,}5\end{pmatrix}\]Dabei ist \(\color{blue}{2{,}5}\) ein Skalar.
Die Skalarmultiplikation\[\color{blue}{-4}\cdot \begin{pmatrix}-1\\-2\\-5\end{pmatrix}=\begin{pmatrix}\color{blue}{-4}\cdot (-1)\\\color{blue}{-4}\cdot (-2)\\\color{blue}{-4}\cdot (-5)\end{pmatrix}=\begin{pmatrix}4\\8\\20\end{pmatrix}\]Dabei ist \(\color{blue}{-4}\) ein Skalar.
Zu den interaktiven Aufgaben → Skalarmultiplikation - Übungsaufgaben
Weiterführende Artikel:
Hat alles, was man braucht: Taschenrechner CASIO FX-991DE X *
Die mit Sternchen (*) gekennzeichneten Verweise sind sogenannte Provisions-Links. Für dich entstehen dabei keine Nachteile!