MathematikDer Differentialquotient an einer Stelle \(a\) einer Funktion gibt die momentane Änderungsrate an dieser Stelle an. Er ist durch den Grenzwert
\[\lim _{b \rightarrow a}\frac{f(b)-f(a)}{b-a}\]
festgelegt. Der Term \(\frac{f(b)-f(a)}{b-a}\) ist dabei der Differenzenquotient. Die momentane Änderungsrate kann auch als die momentane Steigung aufgefasst werden.Aufgepasst! Es ist nicht immer möglich diesen Grenzwert zu berechnen, er existiert in manchen Fällen nicht!
Die Symbole \(\displaystyle \lim _{b \rightarrow a}\) bedeuten, dass sich die Variable \(b\) kontinuierlich dem Wert \(a\) annähert ('lim' steht für Limes, das soviel wie Grenze heißt).
Warum kann man nicht gleich statt \(b\) den Wert \(a\) einsetzen?
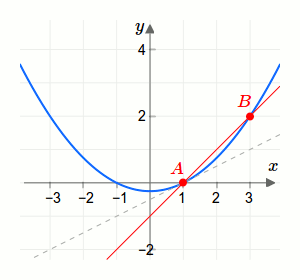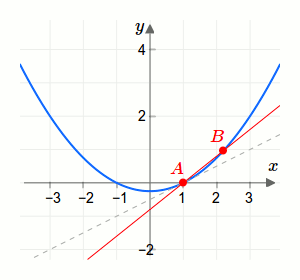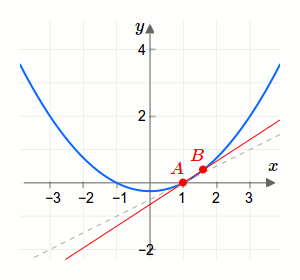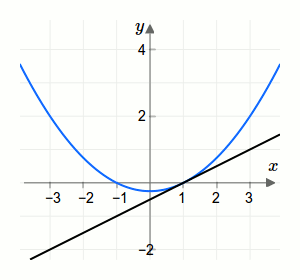
Setzt man im Differenzenquotient \(b=a\), so erhält man Null durch Null. Das ist ein Ausdruck mit dem wir nichts anfangen können und der zudem ungültig ist! Daher nähern wir uns kontinuierlich zu diesem Ausdruck. Die Annäherung vom Differenzenquotient an den Differentialquotienten einer Funktion an einer Stelle \(a\) ist in der folgenden animierten Grafik dargestellt. Dort ist die momentane Steigung durch eine gestrichelte Gerade und die mittlere Steigung durch eine durchgehende Gerade dargestellt.
Es wird oft eine äquivalente Darstellung des Differentialquotienten verwendet. Dafür nennt man die Stelle, an der man die momentane Änderung berechnen möchte \(a=x_0\). Des weiteren ersetzt man \(b=x_0+\Delta x\).Die momentane Änderungsrate bzw. der Differentialquotient einer reellen Funktion \(f\) an einer Stelle \(x_0\) ist durch \[f'(x_0)= \lim _{\Delta x \rightarrow 0}\frac{f(x_0+\Delta x)-f(x_0)}{\Delta x}\] gegeben.
Da dieser Ausdruck so wichtig ist, verwendet man die Notation \(f'(x_0)\). Man kann statt \(f'(x_0)\) auch \(\frac{df(x_0)}{dx}\) schreiben.
Weiterführende Artikel:
Impressum
Datenschutz