Punktwolkendiagramm

Ein Punktwolkendiagramm ist eine grafische Darstellung von Wertepaaren \((x|y)\) und wird meistens dazu verwendet um Zusammenhänge zwischen den Wertepaar-Variablen \(x\) und \(y\) zu erkennen.

Dabei wird jedes Wertepaar als Punkt auf eine Ebene abgebildet bzw. eingezeichnet. Alle Punkte zusammen können dann eine bestimmte Form annehmen, die hier als Wolke bzw. Punktwolke bezeichnet wird. Daher der Name 'Punktwolkendiagramm'. Man sagt oft auch Streudiagramm (engl. scatter plot) zu einem Punktwolkendiagramm. Wichtig ist es, dass der Unterschied zwischen Zusammenhang und Abhängigkeit zweier Variablen verstanden wird. Denn mit einem Punktwolkendiagramm kann man nur den Zusammenhang und nicht die Abhängigkeit zweier Variablen untersuchen. Dazu sind weiter unten zwei Beispiele gegeben.

Wie erkennt man nun einen Zusammenhang zwischen zwei Variablen mittels einem Punktwolkendiagramm?
Anhand der Form der Punktwolke. Wenn beispielsweise die Wolke linienförmig aussieht und geneigt ist (also nicht vollständig waagrecht oder vollständig vertikal), besteht ein Zusammenhang zwischen den Variablen. Wir sehen uns dazu Beispiele an und betrachten danach unterschiedliche Typen von Zusammenhängen.

Beispiele mit Grafiken

Wir untersuchen, ob ein Zusammenhang zwischen dem Alter und dem Preis eines Gebrauchwagens besteht. 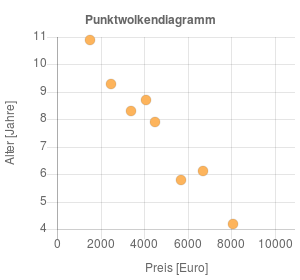Jemand notiert den Preis \(x\) und das Alter \(y\) von verschiedenen zufällig ausgewählten Gebrauchtwagen in eine Liste: \[\begin{array}{c|c} x \text{ [Euro]} & y\text{ [Jahre]} \\ \hline 3400 & 8{,}3 \\ 5700 & 5{,}8 \\ 2500 & 9{,}3 \\ 8100 & 4{,}2 \\ 1500 & 10{,}9 \\ 4100 & 8{,}7 \\ 4500 & 7{,}9 \\ 6700 & 6{,}1 \end{array}\] In der nächsten Grafik sind diese Wertepaare \((x|y)\) in ein Punktwolkendiagramm eingezeichnet. Dabei ist jeder Punkt ein Wertepaar. Wie man sieht sind die Wertepaare nicht zufällig verstreut, sondern bilden eine geneigte, linienförmige Wolke. Damit besteht ein Zusammenhang zwischen \(x\) und \(y\).

Wir untersuchen, ob ein Zusammenhang zwischen der Körpergröße und dem Alter von Kindern bzw. Jugendlichen besteht. 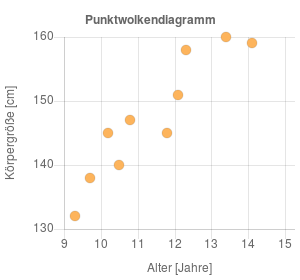Bei einer Gruppe in einem Feriencamp wurden das Alter \(x\) und die Körpergrößen \(y\) der Kinder notiert: \[\begin{array}{c|c} x \text{ [Jahre]} & y\text{ [cm]} \\ \hline 10{,}5 & 140 \\ 12{,}3 & 158 \\ 9{,}7 & 138 \\ 10{,}2 & 145 \\ 13{,}4 & 160 \\ 14{,}1 & 159 \\ 11{,}8 & 145 \\ 12{,}1 & 151 \\ 10{,}8 & 147 \\ 9{,}3 & 132 \end{array}\] In der folgenden Grafik sind diese Wertepaare in einem Punktwolkendiagramm dargestellt. Man kann erkennen, dass ein Zusammenhang zwischen der Körpergröße und dem Alter besteht, da die Wertepaare nicht zufällig verstreut sind, sondern eine geneigte, linienförmige Wolke bilden.

Als nächstes sehen wir uns zwei Beispiele zum Unterschied zwischen Zusammenhang und Abhängigkeit zweier Variablen an.

Man hat durch statistisches Auswerten vieler Facebook-Profile herausgefunden, dass Personen, die eine bestimmte Fernsehserie "geliked" haben, im Schnitt intelligenter sind als eine durchschnittliche Person. Das bedeutet allerdings nicht, dass jede Person nun intelligenter wird, wenn sie zu dieser Fersehserie ein "like" setzt. Es besteht also 'nur' ein Zusammenhang und keine Abhängigkeit. Würde eine Abhängigkeit bestehen, würde man durch ein "like" tatsächlich intelligenter als der Durchschnitt sein bzw. werden!

In den letzten Jahrhunderten hat die weltweite Anzahl an Piraten abgenommen und die globale Durchschnittstemperatur zugenommen. Offenbar gibt es einen Zusammenhang zwischen diesen beiden 'Variablen' (x = Anzahl Piraten, y = globale Durchschnittstemperatur).

Die Klimaerwärmung lässt sich dennoch nicht aufhalten, indem man jetzt viele Menschen dazu bringt Pirat zu werden! Würden die beiden 'Variablen' voneinander abhängig sein, dann müsste es die globale Durchschnittstemperatur senken! Das eine hat aber mit dem anderen nichts zu tun!

Typen der Zusammenhänge

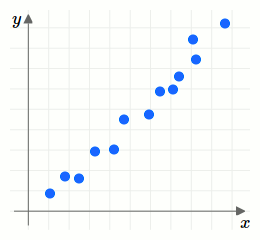
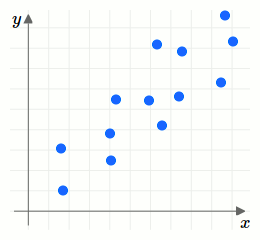
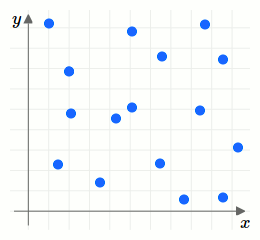
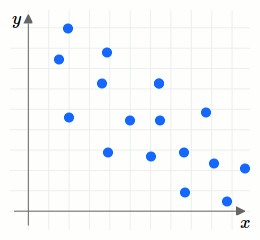
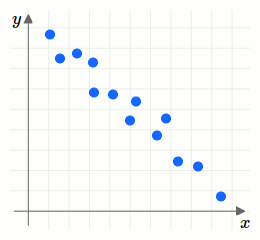
Wir erläutern die verschiedenen Typen durch Betrachten verschiedener Punktwolkendiagramme. Dabei unterscheiden wir zwischen positiven und negativen Zusammenhängen. Ein Zusammenhang ist positiv, wenn der Trend besteht, dass für zunehmenden \(x\)-Wert auch der \(y\)-Wert zunimmt. Ein Zusammenhang ist negativ, wenn der Trend besteht, dass für zunehmenden \(x\)-Wert der \(y\)-Wert kleiner wird.
Weiters unterscheiden wir zwischen starken und schwachen Zusammenhängen. Ist die Punktwolke schmal, so ist der Zusammenhang stark, da er näherungsweise für jedes Wertepaar gleich gegeben ist. Ist die Punktwolke breiter, so gibt es unterschiedlich starke Zusammenhänge für unterschiedliche Wertepaare. Damit ist der Zusammenhang schwach.
Sind die Wertepaare vollständig zufällig verteilt, so ist kein Zusammenhang gegeben.

Punktwolkendiagramm starker positiver Zusammenhang — Starker positiver Zusammenhang zwischen \(x\) und \(y\)

Punktwolkendiagramm schwacher positiver Zusammenhang — Schwacher positiver Zusammenhang zwischen \(x\) und \(y\)

Punktwolkendiagramm kein Zusammenhang — Kein Zusammenhang zwischen \(x\) und \(y\)

Punktwolkendiagramm schwacher negativer Zusammenhang — Schwacher negativer Zusammenhang zwischen \(x\) und \(y\)

Punktwolkendiagramm starker negativer Zusammenhang — Starker negativer Zusammenhang zwischen \(x\) und \(y\)

Zu den interaktiven Aufgaben → Punktwolkendiagramm - Übungsaufgaben

Weitere Diagrammtypen

Weitere Diagrammtypen sind

Quellen: wikipedia.org/wiki/Streudiagramm